austinmw89
- 16
- 0
Problem statement:
The E field measured just above a glass plate is equal to 2 V/m in magnitude and is direct at 45° away from the boundary, as shown in the figure. The magnitude of the E field measured just below the boundary is equal to 3 V/m. Find the angle theta for the field in the glass just below the boundary.
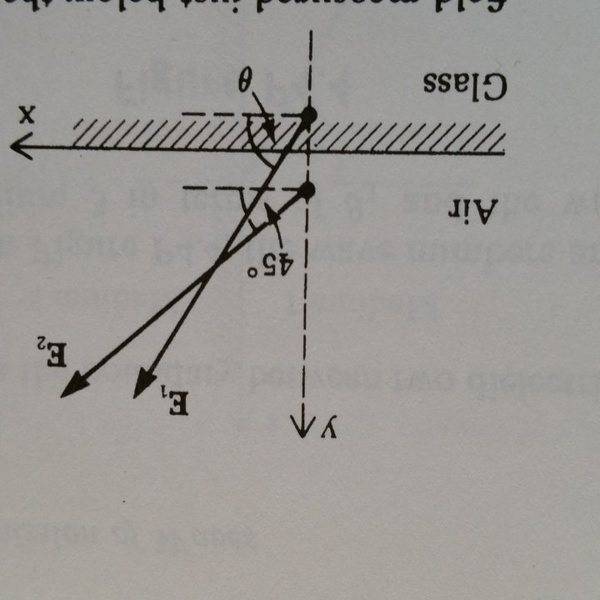
(sorry I don't know why uploading the image flipped it upside down)
I have the solution from the manual for this problem, but I still don't understand it. I'd really appreciate if someone could explain the beginning set-up of the solution:
E_1tan = E_2tan -> E_1cos(theta)=E_2cos(45°) -> cos(theta) = (E_2/E_1)*(sqrt(2)/2) -> theta = 61.9°.
I can follow the math from the second step, but my geometry is pretty rusty and I don't understand how they start with the tangents and also how they go from tangents to cosines.
The E field measured just above a glass plate is equal to 2 V/m in magnitude and is direct at 45° away from the boundary, as shown in the figure. The magnitude of the E field measured just below the boundary is equal to 3 V/m. Find the angle theta for the field in the glass just below the boundary.
(sorry I don't know why uploading the image flipped it upside down)
I have the solution from the manual for this problem, but I still don't understand it. I'd really appreciate if someone could explain the beginning set-up of the solution:
E_1tan = E_2tan -> E_1cos(theta)=E_2cos(45°) -> cos(theta) = (E_2/E_1)*(sqrt(2)/2) -> theta = 61.9°.
I can follow the math from the second step, but my geometry is pretty rusty and I don't understand how they start with the tangents and also how they go from tangents to cosines.
Last edited: