pbonnie
- 92
- 0
Homework Statement
Tan A = -2/6
a) Draw two possible locations on the coordinate axis for the terminal arm of angle A
b) Find two possible values for the measure of angle A and the related acute angle.
Homework Equations
c^2 = a^2 + b^2
SOHCAHTOA
The Attempt at a Solution
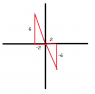
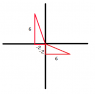
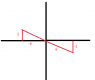
I know that the two possible locations are in quadrants II and IV. But I'm not sure how they're supposed to be drawn? I attached an image of how I think it's supposed to be, but I'm not sure if I did it right.
Also, I'm not sure what angle A represents? Is it the angle IN the triangle? or the angle outside of it?