Angular Acceleration and Projectile Motion

[MyNewPony]

Homework Statement

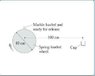
An amusement park game, shown in the figure (see attachment), launches a marble toward a small cup. The marble is placed directly on top of a spring-loaded wheel and held with a clamp. When released, the wheel spins around clockwise at constant angular acceleration, opening the clamp and releasing the marble after making 11/12 revolution.

What angular acceleration is needed for the ball to land in the cup?

Homework Equations

x1 = vcos(theta)t
y1 = y(initial) + vsin(theta)t - 4.9t^2

omega = v/r

a = (omega(final)^2 - omega(initial)^2)/2(delta(theta))

The Attempt at a Solution

1) 11/12 of a revolution = 330 degrees, therefore it is launched at an angle of 30 degrees.
2) It is shot from an initial height of rcos30 = 0.2*sqrt3/2 m
3) It has a range of 1 + rsin30 = 1 + 0.2*1/2 = 1.1 m

I know I'm supposed to find launch velocity from this data but how do I go about doing so?

 

[Doc Al]

The Attempt at a Solution

1) 11/12 of a revolution = 330 degrees, therefore it is launched at an angle of 30 degrees.
2) It is shot from an initial height of rcos30 = 0.2*sqrt3/2 m
3) It has a range of 1 + rsin30 = 1 + 0.2*1/2 = 1.1 m

Sounds good. (I assume that the cup is at the same height as the center of the wheel? Hard to tell from the diagram.)

I know I'm supposed to find launch velocity from this data but how do I go about doing so?

Set up the usual projectile motion equations for vertical and horizontal position as a function of time.

 

[Shutyourmouth]

I'm trying to do this same problem, but I don't know how. I was hoping I could figure it out with some online help, but I don't understand where you got all the equations and such.