Angular acceleration direction, rotating rigid bodies

[binbagsss]

The direction of rotating bodies about a fixed axis.
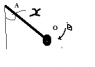
I am confused on how you should regard the the direction of mg sin x, the angular acceleration and the force exerted on the body by the axis, perpendicular to OG ( where O is the fixed axis location and G is the centre of mass of the body).
There are key scenarios in that a rotating body could be at the bottom of its circular motion.
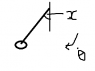
I have attached diagrams indicating both, and have labelled on a direction of angular speed.

Okay so in diagram 1, where the mass is APPROACHING the lowest point, it is speeding up. Taking downward as negative then , I would conclude:
- mg sin x : negative
- Y (force exerted by axis) : positive - you can go either way?
- Angular acceleration, most importantly, I would take this as negative - my reasoning being that the body is moving downward at this point whilst increasing in speed.

In diagram 2 I would conculde:
- mg sin x : negative
- Y (force exerted by axis) : positive - you can go either way?
- Angular acceleration, most importantly, I would take this as negative - my reasoning being that the body is moving upward at this point whilst decreasing in speed.

I asuume that I must be regarding the angular acceleration incorrectly to reach the same conclusion in both cases ! Any assistance, really, really appreciated, thaks a lot ! =]

 

[ehild]

Decide from where you measure the angle. If you measure it from the negative vertical, and define increasing angle counter-clockwise, then the angle is positive in the first figure, but the angular velocity is negative in the direction of the motion (the angle decreases). You get the direction of angular acceleration from the direction of torque. Gravity would turn the body clockwise, so it is negative. And you are right, the angular velocity is negative and increases in magnitude also means that the angular acceleration is negative.
In figure on the right, the angle is negative, and the angular velocity is negative, but decreasing in magnitude, so the angular acceleration is positive. Also, the torque of gravity would rotate anti-clockwise.

ehild

 

[binbagsss]

Decide from where you measure the angle. If you measure it from the negative vertical, and define increasing angle counter-clockwise, then the angle is positive in the first figure, but the angular velocity is negative in the direction of the motion (the angle decreases). You get the direction of angular acceleration from the direction of torque. Gravity would turn the body clockwise, so it is negative. And you are right, the angular velocity is negative and increases in magnitude also means that the angular acceleration is negative.
In figure on the right, the angle is negative, and the angular velocity is negative, but decreasing in magnitude, so the angular acceleration is positive. Also, the torque of gravity would rotate anti-clockwise.

ehild

This sounds extremely promising, just about to give it a shot, quick question...and then am I right in thinking that you can consider Y to be in either direction, and the rest will reveal, or should you logically apply knowledge of vertical circular motion ?.. I have attached a diagram, in the way that for this direction of angular speed, in the 2 right quadrants to move upward aainst mg, the force exerted by the axis on the body must be upward, but then in the 2 left quadrants, y could be in either direction or?

Ahh, also sorry I should have been a lot clearer. It is force equations parallel and perpendicular to the line OG which I am trying to establish - therefore should I be considering the mg component force wise or torque wise - force wise, the components always negative, torque wise, it could go both ways...

Thank you so much, really , really appreciate it !

 

[ehild]

I don't quite get you. Gravity points downward. The normal force at the axis of rotation can have any direction, to ensure that the body stays attached to it.

It would be more clear if you wrote the whole problem with the attempt of solution. I could tell you if you are right or not.

ehild

 

[binbagsss]

A uniform circular disc has mass M and diameter AB of length 4a, the disc can rotate in a vetical plane about a fixed smooth horizontal axis perpendicular to the plane of the disc through point D of AB, AD = a.
The disc is released from rest with AB horizontal, find the component perpendicular to AB when AB makes angle pheta with the downward vertical.

- Taking the clockwise direction as positive, speed is increasing so the acceleration is
- considering torques, I would conclude that the mg sin phetais also positive.
- however, considering forces, the mg compoennt is negative.

The correct solution is:
- Y - mg sin pheta = Ma pheta.

 

[ehild]

.
The disc is released from rest with AB horizontal, find the component perpendicular to AB when AB makes angle pheta with the downward vertical.

The component of what?

ehild

 

[binbagsss]

The component of what?

ehild

Apologies ! the force exerted on the axis.

 

[binbagsss]

Apologies ! the force exerted on the axis.

*by the rotating body
Previous post should read +y-mgsinpheta = masinpheta. (apologies)

 

[ehild]

What is Ma pheta?

A figure would make the problem more clear. Enclosing an angle with the downward vertical can be both clockwise and anti-clockwise. If it is clockwise, the speed decreases with time at 40° position. The usual thing is to measure angles anti-clockwise. The disk rotates clockwise. That might cause confusion with the signs. Can you show a figure that explains what directions of theta and Y you took as positive?
If Y is the force the body exerts on the axis, then the axis exerts the opposite force on the body.

By the way, the angles are denoted by Greek letters. There are such ones as phi and theta. There is no "pheta"

ehild