Angular Acceleration of A Rigid Rod

[tzacher]

Homework Statement

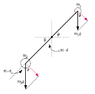
A rigid rod of mass 3.50 kg and length of 2.70 m rotates in a vertical (x,y) plane about a frictionless pivot through its center. Particles m1 (mass=4.70 kg) and m2 (mass=2.60 kg) are attached at the ends of the rod. Determine the size of the angular acceleration of the system when the rod makes an angle of 46.1o with the horizontal.

Homework Equations

I = (1/12)ML^2 + MR^2 + MR^2
τ = Iα

The Attempt at a Solution

So I tried using the moment of inertia to find the I of the rod and each mass, then tried plugging that into the torque equation, but I can't seem to figure out what the torque equation is supposed to be. I tried to have τ=m1gL1sinθ-m2gL2sinθ, but that didn't work out. Can anyone help me?

 

[gneill]

Perhaps you could spell out more of your calculation details. Also, verify the location of the angle θ in the triangles you've constructed for the torque calculations.

 

[tzacher]

Alright so for moment of inertia, I had:

I = (1/12)(3.5)(2.7)^2 + 4.7(.675)^2 + 2.6(.675)^2

And then my torque was:

T = (.675)(9.81)(4.7)sin(46.1) + (.675)(9.81)(4.7)sin(46.1)

I'm not quite sure about the torque calculation being correct.

 

[gneill]

Alright so for moment of inertia, I had:

I = (1/12)(3.5)(2.7)^2 + 4.7(.675)^2 + 2.6(.675)^2

And then my torque was:

T = (.675)(9.81)(4.7)sin(46.1) + (.675)(9.81)(4.7)sin(46.1)

I'm not quite sure about the torque calculation being correct.

Yes, there's a bit of a problem with your torque calculation. Here's a diagram of the situation

Well, it's one of the possible situations; The problem doesn't specify which mass is on which end of the rod or which one is elevated above the pivot, or even on which side of the pivot the rod is elevated! So I suppose that you can assume they want the magnitude of the acceleration without specifying its direction.

Note where the angle θ appears in the force triangles relating the weights of the masses and the components perpendicular to rod. What trig function is applicable to find that component? Note also the directions that the torques have with respect to each other. Do they aid or oppose each other?

 

[tzacher]

I don't think the direction matters, it rarely does.

So how would I find the torque? They're both going downwards, but I know that the larger mass is going to exert more of a torque. So would that make the torque:

T = r*m1g*cos(θ) - r*m2g*cos(θ)

 

[gneill]

Yes, that looks better. Take the absolute value of the difference to indicate that direction is being ignored.