Angular Acceleration of Cord Problem

[RoyalFlush100]

Homework Statement

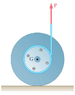
"A drum of 60-mm radius is attached to a disk of 120-mm radius. The disk and drum have a total mass of 6 kg and a combined radius of gyration of 90 mm. A cord is attached as shown and pulled with a force P of magnitude 20 N. The disk rolls without sliding. Determine the minimum value of the coefficient of static friction compatible with this motion."

I have attached the image below

Homework Equations

T = Iα

The Attempt at a Solution

Known forces:
W = (6 kg)(9.81 N/kg) = 58.86 N, downwards, at G
First, because the system is not accelerating in the y direction we know that:
N = W - P = 58.86 - 20 = 38.86 N
Friction then will equal:
f = 38.86μ

Moment of Inertia:
I = (6 kg)(0.09 m)^2 = 0.0486 kg*m^2

So, now the sum of all torques:
T = -(0.12 m)(38.86μ) = (0.0486 kg*m^2)α

I'll need angular acceleration of the middle disc. What would I need to do to find that? Also, I'm assuming there has to be another horizontal force (presumably at G), how would that factor in?

 

[TomHart]

Moment of Inertia:
I = (6 kg)(0.9 m)^2 = 4.86 kg*m^2

Check your conversion from 90 mm to meters.

So, now the sum of all torques:
T = -(0.18 m)(38.86μ) = (4.86 kg*m^2)α

Where did 0.18 meter come from. It says the disk is 120 mm, which converts to 0.12 meter.
Also, in summing torques, doesn't the force P produce a torque?

Also, I'm assuming there has to be another horizontal force (presumably at G), how would that factor in?

I'm not sure where that other horizontal force would come from. P is vertical, weight is vertical, normal is vertical, and friction is horizontal. Is there anything else other than those?

 

[RoyalFlush100]

Check your conversion from 90 mm to meters.Where did 0.18 meter come from. It says the disk is 120 mm, which converts to 0.12 meter.
Also, in summing torques, doesn't the force P produce a torque?

I'm not sure where that other horizontal force would come from. P is vertical, weight is vertical, normal is vertical, and friction is horizontal. Is there anything else other than those?

Okay, I edited the OP to fix the length measurements.

So the torque now should be:
T = -(0.12 m)(38.86μ) + (0.06 m)(20 N) = (0.0486 kg*m^2)α

And disregard what I said about the horizontal forces, it makes sense now.

However, I am not sure how to calculate angular acceleration in this case. Or is angular acceleration 0?

 

[TomHart]

However, I am not sure how to calculate angular acceleration in this case. Or is angular acceleration 0?

You need to use the equation that relates angular acceleration to linear acceleration. If you are trying to find the minimum coefficient of friction that will produce no slipping, that indicates that there will be acceleration.

 

[RoyalFlush100]

You need to use the equation that relates angular acceleration to linear acceleration. If you are trying to find the minimum coefficient of friction that will produce no slipping, that indicates that there will be acceleration.

a = rα.
So in that case:
ma = mrα = (6 kg)(0.06 m)α = 38.86μ --> α = 38.86μ/((6 kg)(0.06 m)) = 10.794444μ
T = -(0.12 m)(38.86μ) + (0.06 m)(20 N) = (0.0486 kg*m^2)α
T = -(0.12 m)(38.86μ) + (0.06 m)(20 N) = (0.0486 kg*m^2)(10.794444μ)
-4.6632μ + 1.2 = 0.52461μ
1.2 = 5.18781μ
μ = 0.231

However, that is being marked as incorrect.

 

[TomHart]

Do you know the correct answer to the problem? I wanted to know if I got it right.

 

[RoyalFlush100]

Do you know the correct answer to the problem? I wanted to know if I got it right.

No, sorry.

 

[TomHart]

ma = mrα = (6 kg)(0.06 m)α

One thing I noticed in your equation: You are using a radius of 60 mm. The angular acceleration is not related to the linear acceleration by the radius of the smaller disk. It is the larger disk that is not slipping on the road surface. So the angular acceleration has to be related to linear acceleration by the 120 mm disk - not the 60 mm disk.

 

[RoyalFlush100]

One thing I noticed in your equation: You are using a radius of 60 mm. The angular acceleration is not related to the linear acceleration by the radius of the smaller disk. It is the larger disk that is not slipping on the road surface. So the angular acceleration has to be related to linear acceleration by the 120 mm disk - not the 60 mm disk.

ma = mrα = (6 kg)(0.120 m)α = 38.86μ --> α = 38.86μ/((6 kg)(0.12 m)) = 53.972222222μ
T = -(0.12 m)(38.86μ) + (0.06 m)(20 N) = (0.0486 kg*m^2)α
T = -(0.12 m)(38.86μ) + (0.06 m)(20 N) = (0.0486 kg*m^2)(53.972222222μ)
-4.6632μ + 1.2 = 2.62305μ
1.2 = 7.28625μ
μ = 0.165

Does this match yours?

 

[TomHart]

Yep, that's what I got.

 

[RoyalFlush100]

Yep, that's what I got.

It got marked right, thanks!