golanor
- 59
- 0
Homework Statement
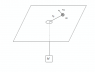
A mass m is laying on a frictionless table and is connected to a mass M with a nonelastic string going through the center of the table. At t=0 the m mass is at a r0 distance from the center of the table, and is moving at a v0 velocity in the tangent direction.
Find the r(t) using conservation of angular momentum and energy.
Homework Equations
conservation of angular momentum and energy.
The Attempt at a Solution
Since the net torque on the system is 0, the angular momentum remains the same, so:
m*r0*v0 = m*r*v
the string constraint:
Δy = Δr => Vy=Vr => Ay = Ar
Initial energy - 1/2*m*(v0)^2
Energy after t seconds: 1/2mv^2+MgΔy+1/2M(Vy)^2+1/2m(Vr)^2
this is as far as I've gotten. I tried using a different version with moment of inertia and angular velocity, but i always get stuck with complicated ODEs which, i think, are not what i should get.
I'm probably missing something, can you tell me what?