- #1
Unperfect
- 4
- 0
Homework Statement
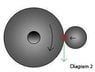
Ok so I have two objects of different masses [itex]{m}_{{1}}[/itex] for the projectile and [itex]{m}_{{2}}[/itex] for the spinning top. The projectile has only translational kinetic energy in the direction of the arrow (see attached image), with [itex]{v}_{{1}}[/itex] and [itex]{v}_{{2}}[/itex] as initial and final linear velocities, respectively the initial velocity is known but not the final one. It collides with a spinning top, which has [itex]{\omega }_{{1}}[/itex] and [itex]{\omega }_{{2}}[/itex] as initial and final angular velocities, the initial being known.
.
Homework Equations
Firstly there is no torque(I have already asked a few people and they mentioned torque), as the perpendicular distance of the projectile from the axis of the spinning top is 0.(so [itex]\tau =r\times F = 0[/itex])
Energy wise: [itex]{E}_{{before}}=\frac {1}{2}I{\omega }_{{1}}^{{2}}+\frac {1}{2}{m}_{{1}}{v}_{{1}}^{{2}}[/itex]
[itex]{E}_{{after}}=\frac {1}{2}{m}_{{1}}{v}_{{2}}^{{2}}+\frac {1}{2}{m}_{{2}}{v}_{{s2}}^{{2}}+\frac {1}{2}I{\omega }_{{2}}^{{2}}[/itex]
vs2 is the final velocity of the spinning top.
The http://en.wikipedia.org/wiki/Elastic_collision" are also relevant.
The Attempt at a Solution
Well I know how to solve collisions, but only when they are exclusively linear or angular.
I have basically used the conservation of energy principle, solving first in 1D(is that possible, or do I have to solve in 2d? And in 2d, how would you do it taking account of the angular velocity of the spinning top?) which obviously left me without answer.
Considering solving in 2D, I based myself on this:
http://www.myphysicslab.com/collision.html
but I am not sure it would work for a spinning top, could anyone advise me on how to use these equations but with a spinning top?
So basically I am a lost, could anyone help out/ give me some possible directions to explore?
Thanks in advance...
PS: This is unrelated but could the admins please remove the automatic adding of the template each time the thread is previewed, its really annoying :) (or maybe its just a problem with vBulletin)
Attachments
Last edited by a moderator: