Angular momentum and moment of inertia

[JulienB]

Homework Statement

Hi everyone! I'm preparing an exam and reviewing some old problems until then, to clear up some misconceptions I might have!
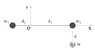
A stiff massless bar is frictionless rotatable about a point O. Two mass points m₁ and m₂ are fixed at its ends, respectively at distances d₁ and d₂. The bar is at rest, when a point-shaped bubble gum hits the mass m₂ perpendicularly with velocity v and sticks on it. (see attached picture) What is the angular velocity of the bar after the collision? Justify your answer. (There is no field of gravity to consider here)

Homework Equations

Moment of inertia, angular momentum

The Attempt at a Solution

So when I see a collision with a fixed rotatable object I think immediately angular momentum:

m⋅v⋅d₂ = I_system⋅ω

The left side describes the motion of the gum relative to O before the collision, while the right side describes the rotation of the system after the gum stuck on m₂.

⇒ ω = m⋅v⋅d₂/I_system

Since the bar is massless, I believe the moment of inertia can be calculated like for two atoms orbiting a point:

I_system = m₁⋅d₁² + (m₂ + m)⋅d₂²

Is that right? If so, my answer would then be:

ω = m⋅v⋅d₂/(m₁⋅d₁² + (m₂ + m)⋅d₂²)

That is all? I am surprised because usually the problems to solve are quite tough.

Extra question: I also tried to solve that with conservation of energy, which gives a different result. But then I thought that in an inelastic collision, there is some loss of energy due to the fact that the gum sticks on the ball, so it can't apply here. Is that assumption correct?

Thank you very much in advance for your answers.

Julien.

 

[TSny]

Looks good except for your calculation of I_system. Should anything be squared there?
I agree with your comments about energy.

 

[JulienB]

Oops yeah I forgot to write the squares, but they are on my paper. I edit the post immediately, thank you for your answer!