Geoanth3
- 3
- 0
Homework Statement
(a) A certain comet of mass m at its closest approach to the Sun is observed to be at a distance r1 from the center of the Sun, moving with speed v1. At a later time the comet is observed to be at a distance r2 from the center of the Sun, and the angle between rvec2 and the velocity vector is measured to be θ. What is v2? Do not worry about italics. For example, if a variable g is used in the question, type g. Use theta for θ, r_1 for r1, r_2 for r2, v_1 for v1 and m as needed.
I'm not sure how to upload diagrams yet, but if I figure it out I will post the diagram itself here. Until then I'll describe it as best I can:
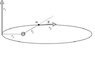
There is a picture of the sun in an ellipse which is very wide and very short, this is the comet's path. The radius from the sun (which is positioned about 1/4 of the way in from the leftmost side) to the leftmost side of the ellipse is r_1. Going up from this point on the ellipse is an arrow labeled v_1 in the positive y direction. r_2 goes from the sun to another point on the ellipse in a NE type direction. There is an arrow coming off of this point labeled v_2 going in the positive x direction. The angle created by r_2 and v_2 is theta (it would be the acute angle as the 2 lines cross).
Homework Equations
L_1=L_2
I_1w=I_2w or r_1Xmv_1=r_2Xmv_2
The Attempt at a Solution
I figured I would set the 2 angular momentums equal after cross multiplying, then solve for v_2 algebraically, but I get the feeling that theta is important, and I'm not sure how it factors in. If someone could help me figure this out it would be so helpful!
 Theta turns out to be important, particularly in your
Theta turns out to be important, particularly in your