Angular velocity and angular momentum

[Northbysouth]

Homework Statement

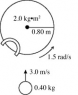
A turntable has a radius of 0.80 m and a moment of inertia of 2.00 kg • m2. The turntable is rotating with an angular velocity of 1.50 rad/s about a vertical axis though its center on frictionless bearings. A very small 0.40-kg ball is projected horizontally toward the turntable axis with a velocity of 3.00 m/s and is moving directly towards the center of the table. The ball is caught by a very small and very light cup-shaped mechanism on the rim of the turntable (see figure). What is the angular velocity of the turntable just after the ball is caught

Homework Equations

L= Iw
The inertia of the turntable = 2.0 kgm^2
The inertia of a solid sphere = 2/5*M*R^2
L_i = initial angular momentum
L_f = final angular momentum (momentum after the ball is caught)
L_id = initial angular momentum of the disc
L_ip = initial angular momentum of the particle
L_fd = final angular momentum of the disc
L_fp = final angular momentum of the particle
w_ft = angular velocity of the turntable after the ball is caught

The Attempt at a Solution

I assumed that Li = Lf

L_i = L_id + L_ip

Li = 2.0kg*1.50 rad/s + 0
Li = 3.50 kgm^2

Similarly, I thought that:
Lf = L_fd + L_fp
L_f = 2.0kgm^2/s*w_ft + 2/5*0.4kg*0.80^2*w_ft

3.50kgm^2/s = 2.1024w_ft
w_ft = 1.66476 kgm^2/s

As you can see this isn't an answer choice. Is it wrong for me to assume that the angular velocity of the particle after it is caught is the same as that of the turntables angular velocity?

 

[Houdini176]

I'm not too sure if I'm right, but hopefully this is one of the answer choices.

After the collision, the ball and the turntable should be turning together.

Ii*Wi=If*Wf

You can just add up the moments of inertia, so:

If=Turntable Moment + Ball Moment
The ball is small enough that we can treat it like a point particle (I see that you multiplied by 2/5, but that only works whenever the axis of rotation is through the diameter of the sphere, in this case the axis of rotation is a radius r from the ball), so ball moment=m*r^2

2.00*1.5=(2.00+0.4*0.8^2)*Wf
Wf=3/(2.256)
Wf=1.33

Please let me know if that's an answer.

 

[Northbysouth]

Yes that is an answer. Thank you

The choices, which I forget to put in my original post are:

A) 1.33 rad/s
B) 0.75 rad/s
C) 0.30 rad/s
D) 0.50rad/s
E) 0.94 rad/s

 

[Houdini176]

Alright cool.

It looks like you just accidentally multiplied 2*1.5 incorrectly, and used the wrong moment of inertia for the ball.