Angular velocity of three gears attached (showed work)

Join the discussion
Registration is free. Ask a follow-up in this thread, or start your own.
Sign up Log in
11 replies · 11K views
howru
Messages
9
Reaction score
0
1. Homework Statement [/b]
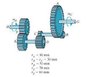
The operation of “reverse” for a three-speed automotive transmission is illustrated schematically in the figure.
If the shaft is turning with an angular velocity of Wg= 30 rad/s, determine the angular velocity of the drive shaft H. Each of the gears rotates about a fixed axis. Note that gears A and B , C and D , E and F are in mesh. The radius of each of these gears is reported in the figure.

Homework Equations


velocity=w * r (w is angular velocity)
"C:\Users\apoorva\Pictures\gears.jpg"[/URL]

[h2]The Attempt at a Solution[/h2]

So the angular velocity of shaft G is 30 rad/s.
I know that the velocity of B and A are same.
V[SUB]g[/SUB]=30(0.09)=2.7 m/s=V[SUB]a[/SUB]
W[SUB]a[/SUB]R[SUB]a[/SUB]=W[SUB]b[/SUB]R[SUB]b[/SUB]
2.7/0.03=90 rad/s =Wb

angular velocity of W[SUB]b [/SUB]and W[SUB]c[/SUB] is the same--> 90 rad/s

V[SUB]c[/SUB]=V[SUB]d [/SUB]so W[SUB]c[/SUB]R[SUB]c[/SUB]=W[SUB]d[/SUB]R[SUB]d[/SUB]
90(.3)=W[SUB]d[/SUB](.05)
W[SUB]d[/SUB]=54 rad/s

W[SUB]d[/SUB]R[SUB]d[/SUB]=W[SUB]e[/SUB]R[SUB]e[/SUB]
54(.05)=W[SUB]e[/SUB](.07)
W[SUB]e[/SUB]=38.6 rad/s

W[SUB]e[/SUB]R[SUB]e[/SUB]=W[SUB]f[/SUB]R[SUB]f[/SUB]
38.6(.07)=W[SUB]f[/SUB](.06)
W[SUB]f[/SUB]=45.03 rad/s

Therefore W[SUB]h[/SUB]=45.03 rad/s

But I keep getting the answer wrong and I don't know what I am doing.
 

Attachments

  • gears.jpg
    gears.jpg
    9.2 KB · Views: 1,537
Last edited by a moderator:

Discussion

Physics news on Phys.org
i don't the link is working, but I posted an attachment which is at the end of the post called "gears"
 
howru said:
So the angular velocity of shaft G is 30 rad/s.
I know that the velocity of B and A are same.
Vg=30(0.5)=2.7 m/s=Va

How did you multiply 30 and .5 and get 2.7?
 
MHrtz said:
How did you multiply 30 and .5 and get 2.7?

I meant 30*(.09)=2.7
not 0.05. sorry about that. I changed it in my post.
Because r=0.09 m is the radius of gear A
 
I think I can help you out. I think you need to use gear ratios.

The speeds of gears can be determined by their gear ratio

If a particular gear moves at say 30 rad/s and has a radius of 4 and that same gear moves another with a radius of 6 than you can find the speed of the second gear by using a ratio

Gear ratio = Radius of larger gear/radius of smaller gear

In this case the gear ratio would be 1.5:1. This means that whenever the first gear rotates 1 and half times the second gear rotates only once.
 
MHrtz said:
I think I can help you out. I think you need to use gear ratios.

The speeds of gears can be determined by their gear ratio

If a particular gear moves at say 30 rad/s and has a radius of 4 and that same gear moves another with a radius of 6 than you can find the speed of the second gear by using a ratio

Gear ratio = Radius of larger gear/radius of smaller gear

In this case the gear ratio would be 1.5:1. This means that whenever the first gear rotates 1 and half times the second gear rotates only once.

how did you get 1.5:1. is from using your numbers or the radius from my problem?

Ok, looking from my problem

Shaft G is 30 rad/s and gear A has the same angular velocity because the shaft is connected to gear A. Radius of gear A is 0.09 meters.

The second gear is B and it's radius is 0.03.
Gear ratio=0.09:0.03 which is 3:1, right?
then I would use that to find my velocity?
So speed of Gear B is=30(3)-->90 rad/s.

Then Gear B and Gear C are the same because the radius is the same.

So Gear C has 90 rad/s which has a radius of 0.03m.
Gear D has 0.05m.
Gear ratio=0.05:0.03--> 1.67:1
then speed of Gear D is (1.67m)(90)=150
..etc.
right. that's the idea?

I understand what you are saying and I'm going to do that. but I'm a little confused about the ratios.

how do you simplify ratios with decimals: so from above .05:.03, would it 1.67:1
OR since .05/.03 is 5/3, would it 3:5
 
never mind you got 1.5 by 6/4.

I got it. just ignore my ratios questions.
thanks for your help.
 
Well if 90mm is 3 times as big as 30mm than that is a ratio of 3:1. Likewise if a gear is .05m and the other is .03m than it is a 5:3 ratio. a 5:3 ratio is the same as a 1.67:1 ratio mathematically.
 
What book are you using? Are using Engineering Mechanics: Dynamics (12th edition) by Hibbeler because if you are then Wg is incorrect. it should be 60rad/s not 30rad/s.
 
MHrtz said:
What book are you using? Are using Engineering Mechanics: Dynamics (12th edition) by Hibbeler because if you are then Wg is incorrect. it should be 60rad/s not 30rad/s.

i'm using the 11th edition but my homework is on masteringengineering.com so sometimes the website changes the numbers.