crossword.bob
- 11
- 4
- TL;DR Summary
- Looking for an explanation of one term in the Compton's original derivation of X-ray scattering
In Compton's 1923 paper on X-rays scattering from light elements, he presents the following diagram:
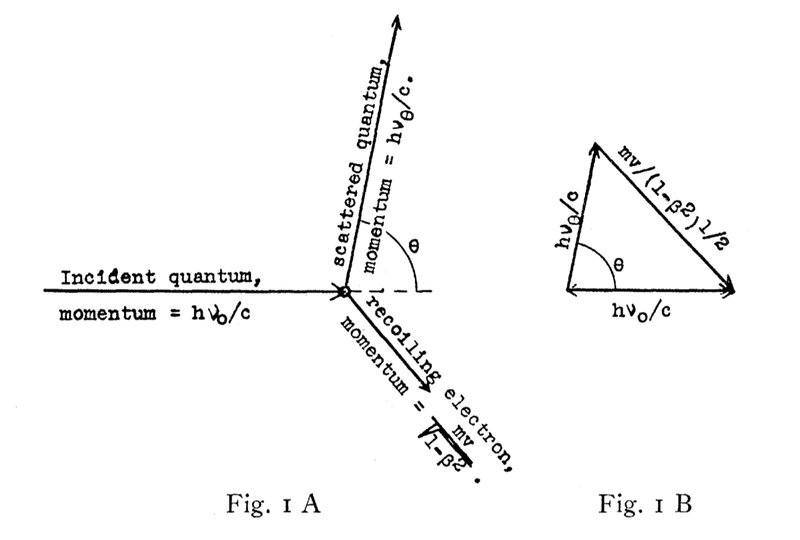
Here, ## h\nu_0/c ## is the momentum of the incident photon, ## h\nu_\theta/c ## is that of the scattered photon and ## mv/(1-\beta^2)^{1/2} ## is that of the recoiled electron. He uses this to express conservation of momentum as $$\left(\frac{m\beta c}{\sqrt{1-\beta^2}}\right)^2 = \left(\frac{h\nu_0}{c}\right)^2 + \left(\frac{h\nu_\theta}{c}\right)^2 + 2 \frac{h\nu_0}{c}\cdot\frac{h\nu_\theta}{c}\cos\theta.$$
I probably shouldn't obsess over details here, but the plus sign on the ##\cos## term is annoying me. Is this not just a simple invocation of the cosine rule? Is one of the terms taken to be negative?
Here, ## h\nu_0/c ## is the momentum of the incident photon, ## h\nu_\theta/c ## is that of the scattered photon and ## mv/(1-\beta^2)^{1/2} ## is that of the recoiled electron. He uses this to express conservation of momentum as $$\left(\frac{m\beta c}{\sqrt{1-\beta^2}}\right)^2 = \left(\frac{h\nu_0}{c}\right)^2 + \left(\frac{h\nu_\theta}{c}\right)^2 + 2 \frac{h\nu_0}{c}\cdot\frac{h\nu_\theta}{c}\cos\theta.$$
I probably shouldn't obsess over details here, but the plus sign on the ##\cos## term is annoying me. Is this not just a simple invocation of the cosine rule? Is one of the terms taken to be negative?