Aparent non-trivial geometry question

[oakwind]

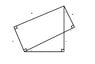
1. I'm looking for the value of "C". All starting information is in the first attachment.



2. Formulas needed are believed to be Pythagoras theorem and trigonometry.



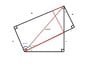
3. "The attempt at a solution": This would be the second attachment. I've wracked my brain for hours and have come to the conclusion I'm either missing something simple or this will involve more than just geometry and trigonometry. The 2 red triangles were suggested by another user whom I suspect didn't look at it hard enough to realize it didn't get any closer to the solution.

What I do know:
-Sides of rectangle are 60 X 10
-Red triangles are similar
-It is solvable as there is no alternative solutions
-Angles A and B are the same

 

[haruspex]

Can you see a pair of similar triangles in the original diagram? I can easily get an equation for C, but it's a quartic. Are you expected to extract the roots of quartics?

 

[oakwind]

Sure, the two triangles in the first diagram are similar. But with only one known value for both, (4 ,10) I know of no way to derive the length of c.

I'm not sure what "extract he roots of quartic" means.

 

[haruspex]

Let the length of the side below A be x. Get a relationship with C from the similar triangles. Get another one between those two (and no other unknowns) using Pythagoras.
A quartic is a polynomial with fourth powers. Extracting the roots of a polynomial means finding the solutions to polynomial = 0.

 

[oakwind]

I've read what you wrote at least 20 times, as best I can tell your trying to lead me to:

4/X = C/10

This isn't a homework problem it's just something I run into on construction jobs often. I think your trying to get me to figure it out, but I guess I have holes in my education preventing me from solving it. Any way I could get a formula that could get me headed in the right direction?

 

[haruspex]

your trying to lead me to:
4/X = C/10

Yes. And the other equation is √(X²+4²)+C=60 (ok?).
That expands to X²+16 = (60-C)²
Substituting X = 40/C from the first equation gives you a quartic in C. There is a formula for solving quartics - you'll find it on the net somewhere - but it's messy.