Application of the Dot Product (Arfken and Weber)

[rwc0613]

Homework Statement

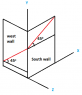
A pipe comes diagonally down the south wall of a building, making an angle for 45 degrees with the horizontal. Coming into a corner, the pipe turns and continues diagonally down a west facing wall, still making an angle of 45 degrees with the horizontal. What is the angle between the south wall and west wall sections of the pipe?

Homework Equations

Dot products invariance under the rotation of a coordinate system

The Attempt at a Solution

My main problem is actually visualizing the question. I feel as if it just an application of the parallelogram rule for addition of vectors and then finding the angle. Arfken says the solution is 120 degrees.

 

[cupid.callin]

consider the red line as pipe in pic.

can you find the unit vectors along the 2 pipes?

 

[gneill]

Write Cartesian vectors for both sections of the pipe (you don't have to be particular about their magnitudes as long as the resultants are in the correct 3D directions).

What do you know about the relationship between the dot product of two vectors and the angle between them?

 

[rwc0613]

Well the relationship between the two vectors in terms of the magnitudes is A dot B=ABcos(theta)=A1B1+A2B2+...+AnBn

 

[gneill]

So, if you can compose two vectors in the directions of the pipes, you can form the dot product directly from its components (A1B1+A2B2+...+AnBn) and also as a product of the vector magnitudes and the cosine of the angle between the vectors. You should be able to solve for the angle, right?

 

[rwc0613]

Okay thanks a bunch guys! I got it!