Applying Kirchoff's Voltage Law to a circuit

[David Day]

Homework Statement

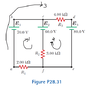
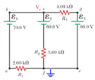
Using Kirchhoff’s rules, (a) find the current in each
resistor shown in Figure P28.31 and (b) find the potential
difference between points c and f.

[/B]

Homework Equations

[/B]
Σ ΔV = 0 (KVL)

The Attempt at a Solution

[/B]
I have been trying to set up a system of equations for the three loops as shown in the picture, but I can't seem to get the right numbers. I was able to get the currents using mesh-current analysis; they are 0.38 mA, 3.08 mA, and 2.69 mA for resistors 1, 2 and 3, respectively. However, I would like to know what mistake I'm making in applying basic KVL to the loops. The equations I get for each loop are:

L1: 70V - 60V - V2 - V1 = 0

L2: 60V - V3 - 80V + V2 = 0

L3: 70V - V3 - 80V - V1 = 0

where V1, V2, and V3 correspond to the voltages at R1, R2, and R3, respectively.

One issue I have noted but am unsure of is whether or not V2 in the second equation should be positive or negative. If I assume the current is flowing downward across R2 it is negative in equation 1. Therefore, I should continue to assume current is flowing downward across R2, which would mean V2 is positive for equation 2. Is that correct?

Any help would be greatly appreciated!

EDIT:

I see now that my equations are not providing enough information to solve for the variables. If I solve for V3 in equation 3 and plug that into equation 2, my equation 2 is just the same equation 1. I'm not sure where to go from this point...

EDIT:

I found my problem. I was missing an equation, I1 = I2 + I3. Using this to solve the system of equation yields the correct results.

 

[vela]

One issue I have noted but am unsure of is whether or not V2 in the second equation should be positive or negative. If I assume the current is flowing downward across R2 it is negative in equation 1. Therefore, I should continue to assume current is flowing downward across R2, which would mean V2 is positive for equation 2. Is that correct?

Yes, that's right.

 

[CWatters]

One issue I have noted but am unsure of is whether or not V2 in the second equation should be positive or negative.

You have it right but it's good practice to mark voltage arrows on the circuit before starting to write the equations.

 

[gneill]

I found my problem. I was missing an equation, I1 = I2 + I3. Using this to solve the system of equation yields the correct results.

Yup, that's a KCL equation. It might be useful to note that this problem can be solved by writing just one equation using the analysis method based on KCL called nodal analysis. Since the problem has been solved by the OP and it's been several weeks, I can offer up this alternative approach.

Choose node $f$ as the common reference point and write the node equation for node $c$ :

$$\frac{V_c - 70}{2000} + \frac{V_c - 60}{3000} + \frac{V_c - 80}{4000} = 0$$
Each of the terms in the node equation represents a current leaving the node by one of the node branches (i.e. KCL for the node).

Then just solve for $V_c$, which will be the potential at node $c$ with respect to node $f$.