I Are electron bands symmetric in the reciprocal space?

[dRic2]

Hi, in the lecture notes my professor gave us, it is stated that, due to Kramers theorem, the energy in a band must satisfy this condition:
$$E(-k) = E(k)$$
But, judging from actual pictures of band structures I don't find this condition to be true. Here's a (random) picture

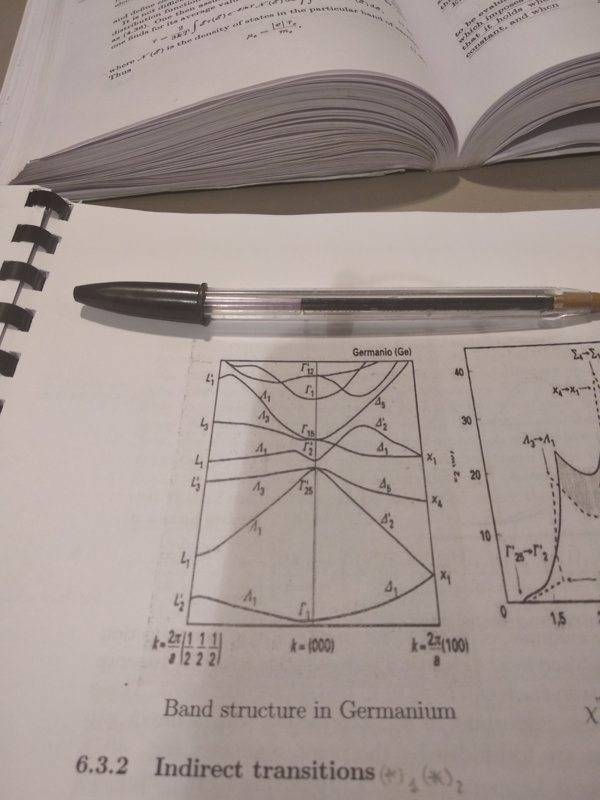
I guess it looks "kind of" symmetric in the lower bands, but I wouldn't certainly call it that way.

 

[MisterX]

I am not sure you know how to read the diagram correctly. The part left of the middle is actually a different direction or slice than the right half of the diagram. That is typical situation for energy band diagrams. Instead of just plotting how the energy bands go along one direction, it takes a path through k space. Often points on the path are labeled with letters like $\Gamma$, but in your case it seems to have indicated the direction with vectors. I borrowed this diagram for education purposes. So you would not see in the diagram what happens if you keep going from M to $\Gamma$ until the end, because once you hit $\Gamma$ the path actually turns up to Z. They do this so a 2D plot can show what happens in multiple directions, but it won't show the symmetry you're seeking.

 

[dRic2]

1000 times thank you. I didn't even notice that the Miller indexes are different.