Area between curves integration problems

[clairez93]

Homework Statement

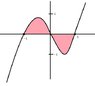
1. Set up the definite integral that gives the area of the region. (See attachment)

f(x) = 3(x^3-3)
g(x) = 0

2. Use integration to find the area of the triangle having the given vertices: (0,0), (a, 0), (b,c)

Homework Equations

The Attempt at a Solution

1.

\int^{0}_{-1}3(x^{3}-x) dx -- \int^{1}_{0}3(x^{3}-x) dx

Somehow the answer key says that this later becomes

-6 \int^{1}_{0}(x^{3} -x) dx

But I can't really see at the moment why that is.


2.

Equations of lines:
y = \frac{c}{b-a}(x-a)

y = \frac{c}{b}x

Area:

\int^{c}_{0}(\frac{c}{b-a}(x-a) - \frac{c}{b}x) dx

\frac{c}{b-a}\int^{c}_{0}(x-a) dx - \frac{c}{b}<br />\int^{c}_{0}x dx

= \frac{c}{b-a}[\frac{x^{2}}{2} - ax]^{c}_{0} - \frac{c}{b}[\frac{x^{2}}{2}

= \frac{c}{b-a}[\frac{c^2}{2} - ca] - \frac{c}{b}(\frac{c^{2}}{2})

= \frac{c^{3}}{2(b-a)} - \frac{c^{2}a}{b-a} - \frac{c^{3}}{2b}

= \frac{bc^{3} - 2abc^{2} - (b-a)c^{3}}{2b(b-a)}

= \frac{ac^{2}(-2b+c)}{2b(b-a)}


If anyone is willing to decipher this and help, it'd be much appreciated.

If the way I typed the Latex is confusing, let me know and I'll scan in my handwork. :]

 

[Дьявол]

1. Area of region

S=\int_{a}^{b}(f(x)-g(x))dx

Now, a and b are the intersection points of the functions f(x) and g(x).

0=3x(x²-1)

There are three intersection points, x₁=0, x₂=1, x₃=-1

Your integral that you need to solve is:

\int_{-1}^{1}(3(x^3-x)-0)dx

2. Area of triangle

You wrote the lines between the points (0,0) and (b,c), and (a,0) with (b,c).

But you forgot one function which is between (0,0) and (a,0).

That function is y=0.

As you can see the intersection points with this line with the others, are x₁=a and x₂=0.

So your original integral would be:

<br /> \int^{a}_{0}<br /> (\frac{c}{b-a}(x-a) - \frac{c}{b}x) dx

Regards.

 

[Elucidus]

Homework Statement

1. Set up the definite integral that gives the area of the region. (See attachment)

f(x) = 3(x^3-3)
g(x) = 0

I see no attachment so I need some clarification. Are you being asked to find the area of the region bound between the curves y=3(x^3-x) and y=0 or between y=3(x^3-3) and y=0 as you originally stated?

Assuming it's y=3(x^3-x), as mentioned the intersections between these two curves occur for x = -1, 0, and 1. The area between the curves is

\int_{-1}^{1}\left| 3(x^3-x) \right|\;dx.[/itex]​

<br /> <br /> Without the absolute value, the integral would be 0, which I doubt is what you seek.<br /> <br /> --Elucidus

 

[clairez93]

Yes I apologize, I have uploaded the attachment now. It is indeed the area between the curves. Why is it however the absolute value? And how did the answer key come up with a value of

-6 \int^{1}_{0}(x^{3} -x) dx?

 

[Elucidus]

Yes I apologize, I have uploaded the attachment now. It is indeed the area between the curves. Why is it however the absolute value? And how did the answer key come up with a value of

-6 \int^{1}_{0}(x^{3} -x) dx?

I seem to not be able to see your attachment - I may be having browser trouble. I am going to try attaching a graph of y=3(x^3-x).

The reason for the absolute value is that the integral

\int_{-1}^{1}3(x^3-x)\;dx​

finds the area under the curve. The part of the curve above the x-axis to the left of the y-axis is going to evaluate as positive area whereas the part of the curve that is in the 4^th quadrant is going to evaluate as negative area. Since this curve is radially symmetric these two areas will be exact opposites and will cancel out giving an answer of 0.

The absolute value guarantees that one is finding the area between the curves.

The theorem is basically: If f and g are continuous on [a, b] and f(x) \geq g(x) for all x in [a, b] then the area between the curves y=f(x) and y=g(x) for a \leq x \leq b is

\int_a^b \left[ f(x)-g(x) \right] \; dx.​

The issue here is that 3(x^3-x) is not greater than 0 throughout [-1, 1].

The reason the answer equals -6 \int_{0}^{1} 3(x^3-x) \; dx has to do with the radial symmetry mentioned earlier.

--Elucidus

 

[Дьявол]

Yes I apologize, I have uploaded the attachment now. It is indeed the area between the curves. Why is it however the absolute value? And how did the answer key come up with a value of

-6 \int^{1}_{0}(x^{3} -x) dx?

Yep, Eluclidus gave you the answer. But I will give you a tip.

Since the area is always positive number and in the expression

\int_{-1}^{0}3(x^3-x)dx - \int_{0}^{1}3(x^3-x)dx

the area of the curve is negative i.e -\int_{0}^{1}3(x^3-x)dx, you need to rewrite the equation in the form:

|\int_{-1}^{0}3(x^3-x)dx| + |\int_{0}^{1}3(x^3-x)dx|

Or as you can see the curves have same area, so the whole area would equal 2*(area of one of the curves).

As you can see \int_{0}^{1}3(x^3-x)dx represents the area of one of the curves. So the whole area would be:
2*\int_{0}^{1}3(x^3-x)dx=2*3\int_{0}^{1}(x^3-x)dx=6\int_{0}^{1}(x^3-x)dx

And did you solve the second one?

Regards.

 

[Elucidus]

So the whole area would be:
2*\int_{0}^{1}3(x^3-x)dx=2*3\int_{0}^{1}(x^3-x)dx=6\int_{0}^{1}(x^3-x)dx

And did you solve the second one?

Regards.

The integral above is negative. This is why the answer begins with -6...

--Elucidus

 

[clairez93]

Ah, I see the symmetry, however, why is the integral negative?

 

[Дьявол]

Ah, I see the symmetry, however, why is the integral negative?

Just look at the graph of the function 3(x³-x), x \in [0,1], you will see that its negative.

So you must put minus, because the area is always positive number.

Regards.