How to create a function such that area under curve is 250

[Ocata]

Suppose you have a given area under a curve, say 250, and want to come up with a function that produces this value. How would you do this?

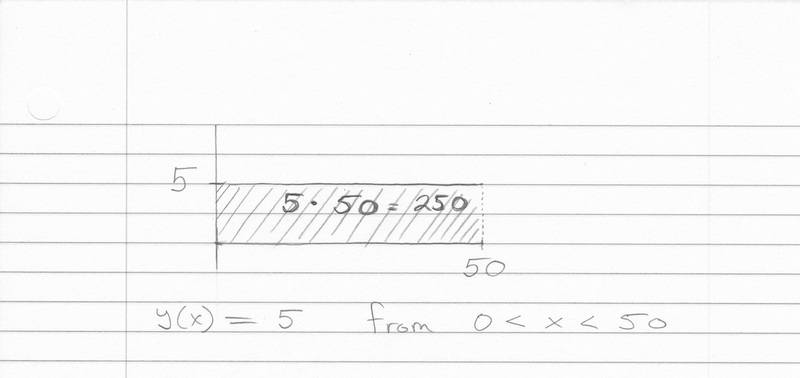
Although I came up with two basic functions as follows:First: Let y (x) = 5 from 0<x<50 , thus length*width = yx = 5*50 = 250.

Second:

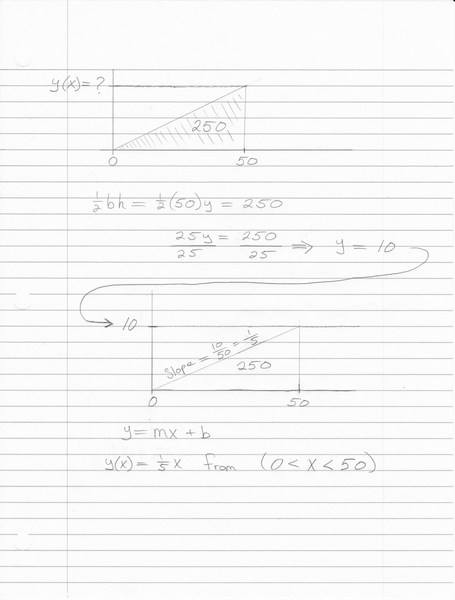
Area of a triangle: 1/2 (base)*(height) = Area

[1/2 (50) (height) = 250] => [25y = 250] => [y = 10]

[y = mx +b] = y(x) = (1/5)x from 0<x<50

I have not been able to figure out how to come up with a "curvy" function like an upside down parabola with roots 0 and 50 on the x-axis with area under the curve being a given value like 250. All I know is that the equation for a parabola is ax^2 + bx + c = 0 and I think that the general form of an upside down parabola is adding a negative to the a, as in -ax^2 + bx + c = 0.

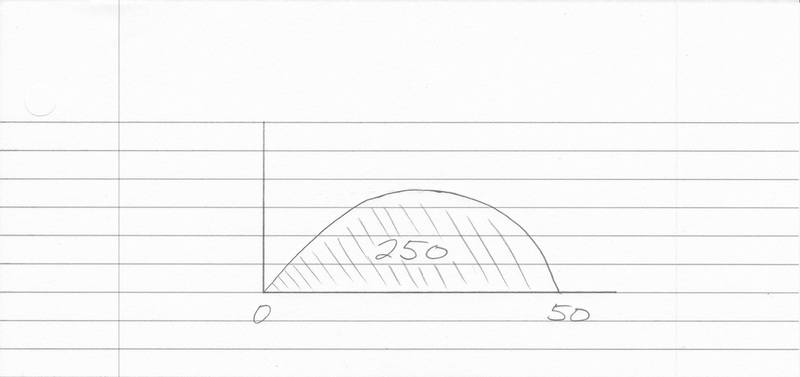
So, my question is, how can I make an upside down parabola that x intercepts 0 and 50, with area under the curve 250?

Thank you

 

[jbriggs444]

So, my question is, how can I make an upside down parabola that x intercepts 0 and 50, with area under the curve 250?

One way to proceed is to start by coming up with the equation for a parabola that has x intercepts at 0 and 50 but which may not have area 250.

The easy way to do that is to use the product of two terms: $(x-0)(x-50)$. This will be a polynomial of the form x^2 + bx + c for some b and c. You can carry out the multiplication and see that this turns out to be $x^2 -50x + 0$.

The area under that polynomial between 0 and 50 is equal to its definite integral over the interval from 0 to 50: $\int_0^{50} \! x^2 - 50x \, \mathrm{d}x$

If you evaluate that integral, you will come up with some figure for area. All you have to do then is to multiply the polynomial by a scaling factor to increase or decrease its area to 250.

 

[Ocata]

One way to proceed is to start by coming up with the equation for a parabola that has x intercepts at 0 and 50 but which may not have area 250.

The easy way to do that is to use the product of two terms: $(x-0)(x-50)$. This will be a polynomial of the form x^2 + bx + c for some b and c. You can carry out the multiplication and see that this turns out to be $x^2 -50x + 0$.

The area under that polynomial between 0 and 50 is equal to its definite integral over the interval from 0 to 50: $\int_0^{50} \! x^2 - 50x \, \mathrm{d}x$

If you evaluate that integral, you will come up with some figure for area. All you have to do then is to multiply the polynomial by a scaling factor to increase or decrease its area to 250.

Thank you jbriggs444,

This is what I have so far:

x = 0 and x = 50
x - 0 = 0 and x - 50 = 0
$(x-0)(x-50) = 0$
$x^2 -50x + 0 = 0$


$\int_0^{50} \! x^2 - 50x \, \mathrm{d}x$

$\frac{1}{3}x^{3} - \frac{5}{2}x^{2}$ from 0 to 50

$\frac{1}{3}(50)^{3} - \frac{5}{2}(50)^{2} - 0$ = 41666.67 - 6250 = 35416.67 = Area under the curveFrom here I'm kind of stuck because I don't know exactly what it means to multiply the polynomial by a scaling factor. Can you please explain what that means and how to do that?

Would it be exactly how it sounds? Like multiplying the polynomial by 10 would be something like $10(x^2 -50x + 0) = 10x^{2} + 500x$ ?

Thank you

 

[Ocata]

P.S. When trying to search "scaling a polynomial," googe returned really complex math publication papers in scientific journals - https://www.google.com/?gws_rd=ssl#q=scaling+a+polynomial&start=0EDIT: Fixed sentence.

 

[jbriggs444]

From here I'm kind of stuck because I don't know exactly what it means to multiply the polynomial by a scaling factor. Can you please explain what that means and how to do that?

Would it be exactly how it sounds? Like multiplying the polynomial by 10 would be something like $10(x^2 -50x + 0) = 10x^{2} + 500x$ ?

Yes, that is exactly what I had in mind. Nothing fancy.

However, you may want to check your equations. The integral of $50x$ is not $\frac{5}{2}x^2$

 

[SteamKing]

Thank you jbriggs444,

This is what I have so far:

x = 0 and x = 50
x - 0 = 0 and x - 50 = 0
$(x-0)(x-50) = 0$
$x^2 -50x + 0 = 0$$\int_0^{50} \! x^2 - 50x \, \mathrm{d}x$

$\frac{1}{3}x^{3} - \frac{5}{2}x^{2}$ from 0 to 50

$\frac{1}{3}(50)^{3} - \frac{5}{2}(50)^{2} - 0$ = 41666.67 - 6250 = 35416.67 = Area under the curveFrom here I'm kind of stuck because I don't know exactly what it means to multiply the polynomial by a scaling factor. Can you please explain what that means and how to do that?

Would it be exactly how it sounds? Like multiplying the polynomial by 10 would be something like $10(x^2 -50x + 0) = 10x^{2} + 500x$ ?

Thank you

There are formulas for calculating the area under a parabolic curve, just like there are formulas for calculating the area of a triangle.

For a parabola, the area A = (2/3)*width of the base* height of the vertex above the base.

In your case, the width of the base = 50 units

https://en.wikipedia.org/wiki/Parabola

 

[Ocata]

Thank you jbriggs444 and SteamKing,I was able to apply your advice and generate the function for the parabola given the x - intercepts and area. Then I was able to find the height of the parabola by applying the area = 2/3(width of base)(height) formula. Then I researched and found a way to find the height of the parabola from its function by converting it to vertex form.x = 0 and x = 50
x - 0= 0 and x - 50 = 0
(x-0)(x-50)
$x^{2} - 50x + 0 = f(x)$ This is function for some parabola$\int_{0}^{50} x^{2} - 50x dx = \frac{1}{3}x^{3} - \frac{50}{2}x^{2}$ from 50 to 0

$\frac{1}{3}(50)^{3}-\frac{50}{2}x^{2} = 41666.67 - 62500 = - 20833.33 =$ Area for some parabola

For a parabola with Area = 250

-20833.33(scaling factor) = 250

s = -.012

if -.012(-20833.33) = 250 then,

-.012$( \int_{0}^{50} x^{2} - 50x dx)$

$-.012(\frac{1}{3}(50^{3}) - (-.012)(\frac{50}{2}(50^{2})$ = -500 + 750 = 250

so the function for the parabola of Area = 250 is:

= $.012(x^{2} - 50x)$ = $-.012x^{2} + .6x$ = f(x)
Area under curve of the parabola $-.012x^{2} + .6x$ = f(x) is:

A = $\frac{2}{3}(x_{1} - x_{0})h$

250 = $\frac{2}{3}(50)h$

$\frac{3}{2}(250)(\frac{1}{50})$ = h = 7.5
From here, I researched a way to find the height of the parabola if I don't know the area under the curve and found that it could found by converting the function of the parabola to vertex form:

$y = -.012x^{2} + .6x$$y = -.012(x^{2} - \frac{.6}{.012}x)$$y + (-.012)(?) = -.012(x^{2} - 50x + (?))$ $(\frac{50}{2})^{2} = 625$$y + (-.012)(625) = -.012(x^{2} - 50x + (625))$

$y = f(x) = -.012(x - 25)^{2} + 7.5$

vertex = (h,k) = (25, 7.5)
Does there happen to be a way to generate a function for a parabola if only given the parabola's height and width of it's base?

For instance, if a parabola has height 7.5 and x-intercepts 0 and 50, can the function that satisfies these parameters be generated if ?

One way I've figured out would be to work in the reverse order, first applying the advice provided by SteamKing:

Area = A = $\frac{2}{3}(x_{1} - x_{0})h$

A = $\frac{2}{3}(50)7.5$ = 250

Then applying the advice provided by jbriggs444:

(x-0)(x-50) = $x^{2} - 50x + 0 = f(x)$

-.012$( \int_{0}^{50} x^{2} - 50x dx)$ = 250

$-.012x^{2} + .6x$ = f(x)I was also wondering if there was an alternate way to find the function of the parabola given only the height and x - intercepts, and supposing the Area = 2/3(width of base)(height) formula is not known?

 

[jbriggs444]

I was also wondering if there was an alternate way to find the function of the parabola given only the height and x - intercepts, and supposing the Area = 2/3(width of base)(height) formula is not known?

Attacking this based on physical intuition rather than algebraicly...

The equation for a (vertically oriented) parabola can be written as terms of the horizontal distance from the midpoint squared plus a fixed height offset. e.g.

$y = h + k(x-m)^2$​

Where h is the height at the midpoint, m is the x coordinate of the midpoint and k is some arbitrarily chosen constant.

So let's use that. We already know the value for h. That is simply the given height.

$h = height$​

The midpoint is the average of the two given intercepts

$m = \frac{i_1 + i_2}{2}$
​

It will be helpful to know the distance from midpoint to intercept. Call that parameter w (short for width).

$w = i_2 - m$ (or, equivalently, $w = m - i_1$)​

Looking back to the formula for our parabola, the value for k must be such that $h + kw^2$ = 0. Solving for k gives

$k = \frac{-h}{w^2}$​

Now, expanding the original equation ($y = h + k(x-m)^2$) to put it into standard form we get

$y = kx^2 - 2kmx + (h+km^2)$
​

Edit: Let's test that for the case at hand. h = 7.5, $i_1 = 0$, $i_2 = 50$

$m = \frac{i_1 + i_2}{2} = 25$
$w = i_2 - m = 25$
$k = \frac{-h}{w^2} = \frac{-7.5}{625} = -.012$
$y = kx^2 - 2kmx + (h+km^2) = -.012x^2 +.6x + 0$​

 

[Ocata]

Looking back to the formula for our parabola, the value for k must be such that $h + kw^2$ = 0. Solving for k gives

$k = \frac{-h}{w^2}$​

How did you determined this: $h + kw^2$ = 0

Trying to understand how the (width of half the base)^2 was determined to be relevant and furthermore how it should be multiplied by an unknown scalar (k) and added to the height should be equal to zero. Why 0? This equation feels like a leap in logic I am not able to make. Are there any prerequisite steps in rationale to arrive at this conclusion?

Thank you.

 

[jbriggs444]

How did you determined this: $h + kw^2$ = 0

Pretend for a moment that the origin of your coordinate system is at the apex of the parabola. Its equation is y = kx^2. At a distance w from the origin its height is h. What value of k is required to make this fit.

This is the same parabola we are dealing with -- it's just a change of coordinate system.

 

[mfb]

Somehow the sign got flipped. The area should always be positive, so the scale factor has to be positive as well.

 

[jbriggs444]

Somehow the sign got flipped. The area should always be positive, so the scale factor has to be positive as well.

If we start with an equation with a positive coefficient on the leading term, the area "under" that parabola will be negative. So the scale factor needs to be negative.

 

[Ocata]

At a distance w from the origin its height is h. What value of k is required to make this fit.

If w = i - m, then how could height h depend on or be determined by a horizontal shift of w? If the apex is at the origin, then the height is zero. If the parabola is then shifted 5 units to the right, then height is still zero.

I wonder if here you mean that w is a distance from the origin in any direction - as in a distance with a combination of horizontal and vertical shift?

 

[jbriggs444]

If w = i - m, then how could height h depend on or be determined by a horizontal shift of w? If the apex is at the origin, then the height is zero.

The height of the parabola segment from the one point where the x intercept had been, through the apex and to the point where the other x intercept had been does not depend on where we choose to put the origin of the coordinate system. It is invariant with respect to translation.
\

 

[Ocata]

Hi jbriggs444,

I just realized, I have no clue what an apex of a parabola is. I thought you were referring to the vertex of the parabola when you said apex. I googled "apex of a parabola" and did not find any information on it.

In the meantime, I did locate another way to solve this which seems much more intuitive to me since it is related to basic algebra:

$y = a(x-h)^{2} + k$ = $y = a(x - 25)^{2} + 7.5$

Pick a point on the line. I can choose (0,0) for this parabola since one of the x-intercepts is 0.

$0 = a(0 - 25)^{2} + 7.5$ = $0 = a(625)^{2} + 7.5$

$\frac{-7.5}{625}$ = -.012 = a

so, $y = -.012(x - 25) + 7.5$From learning this approach, I do see that the $w^{2} = 625$ happens to coming from $(0 - 25)^2 = 625$. Just still not sure how you arrive at $a(w)^2 + k = 0$.

To me $aw^{2} + k = 0$ kind of looks like $a(x - h)^{2} + k = 0$ where x can be 0 or 50. But then the h of vertex (h,k) will always be the midpoint of the parabola, so vertex (h,k) = (m,k)

hmm...okay, maybe I'm starting to see it right about now...or at lease I think I'm starting to see something resembling what you are describing...

Basically, suppose I shift the parabola to the right 10 units. The new x intercepts will be 10 and 60. The new midpoint will be 35, but the difference between the intercepts and midpoint will still be 25. So choosing the point (10, 0) to solve the vertex formula, I end up with the same equation $0 = a(25)^{2}+ 7.5$. So, we arrive at the same scaling factor because intercepts 0 and 50 are equivalent to 10 and 60 when it comes to the intercept minus the midpoint.

So $w = i - m$ will always be the same regardless of where you shift the parabola horizontally, so $w^{2} = (i - m)^{2}$ is equivalent to the value you get when you choose the x - intercept as your point to plug into the vertex formula. Kinda?

 

[HallsofIvy]

First, "apex" of a parabola is just another word for the "vertex" of a parabola, those less often used. It is the "point" of the parabola just as the apex of an angle is the "point" of the angle.

I am not sure what you are trying to do with your last post. Initially, you asked how to find a curve such that the "area under it" (I presume you mean between the curve and the x-axis) is 250. The simplest curve that cuts the x-axis twice, so has an "area under it", is a parabola. You can start with pretty much any parabola. For example, since 0 and 1 are easy numbers, x(1- x)= x- x^2 is a parabola that cuts the x-axis at 0 and 1 and rises above it so has an "area under it".

It is easy to calculate that area: $\int_0^1 x- x^2 dx= \left[\frac{x^2}{2}- \frac{x^3}{3}\right]_0^1= \frac{1}{2}- \frac{1}{3}= \frac{1}{6}$.

That area is, of course, not 250! 250 is $\frac{250}{\frac{1}{6}}= 1500$. So multiply the original function by 1500!

The parabola $1500(x- x^2)= 1500x- 1500x^2$ has area under the curve and above the x-axis 250.

 

[Ssnow]

Depends what kind of function you want consider, if it is exponential $y=e^{x}$ you can consider $\int_{0}^{b}e^{x}d\,x=250$ so $e^{b}-1=250$. The function $e^{x}$ for $x\in [0,\ln{251}]$ is an example ...

 

[Ocata]

First, "apex" of a parabola is just another word for the "vertex" of a parabola, those less often used. It is the "point" of the parabola just as the apex of an angle is the "point" of the angle.

I am not sure what you are trying to do with your last post. Initially, you asked how to find a curve such that the "area under it" (I presume you mean between the curve and the x-axis) is 250. The simplest curve that cuts the x-axis twice, so has an "area under it", is a parabola. You can start with pretty much any parabola. For example, since 0 and 1 are easy numbers, x(1- x)= x- x^2 is a parabola that cuts the x-axis at 0 and 1 and rises above it so has an "area under it".

It is easy to calculate that area: $\int_0^1 x- x^2 dx= \left[\frac{x^2}{2}- \frac{x^3}{3}\right]_0^1= \frac{1}{2}- \frac{1}{3}= \frac{1}{6}$.

That area is, of course, not 250! 250 is $\frac{250}{\frac{1}{6}}= 1500$. So multiply the original function by 1500!

The parabola $1500(x- x^2)= 1500x- 1500x^2$ has area under the curve and above the x-axis 250.

Hi HallsofIvy,

Per jbriggs444's post #2 and subsequent guidance, I understand the step by step logic to come up with a general parabola that cuts the x-axis at a certain points.

For instance, given the example you provided, x = 0 and x = 1.
I would start with (x-0)(x-1) = $(x^{2} - x)$ = $x(x - 1)$
and for an upside down parabola, $-(x^{2}-x)$ = $-x^{2} + x$ = $x - x^{2}$ = $x(1 - x)$

Now, it has taken me a few steps to arrive at the general parabola, but your example with jbriggs444 example for the interval between 0 and 50 has revealed a quick way to generate a general parabola.

For example, given any parabola that cuts the x-axis at 0 and some point $x_{1}$, a general parabola is:$x(x-x_{1})$ or $-(x(x_{1}-x))$

Thank you, by studying the two different sets of x intercepts, [0 and 1] and [0 and 50], both arriving at a function with of the same form, I can now formulate a general function of a parabola step by step or by knowing the final form that the function should have.

And I believe I'm comfortable with coming up with a scaling factor to generate a parabola with a specific area between the curve and the x axis.

What I am still have a bit of uncertainty about is how jbrigg444 was able to create a function of a parabola the way he described, given only the vertex (h,k) and of a given area between the curve and x axis.

Afterwards, I found a method of simply choosing any point on the curve and plugging it into the vertex form of the parabola and solving for the coefficient.

 

[Ocata]

Depends what kind of function you want consider, if it is exponential $y=e^{x}$ you can consider $\int_{0}^{b}e^{x}d\,x=250$ so $e^{b}-1=250$. The function $e^{x}$ for $x\in [0,\ln{251}]$ is an example ...

Actually Ssnow, I'm also interested in the sin function.

Suppose a sin function crosses the x-axis at x = 0 and then at x = 50 and the area under that portion of the curve is 250. How would I find the function that represents these parameters?

 

[Mark44]

Actually Ssnow, I'm also interested in the sin function.

Suppose a sin function crosses the x-axis at x = 0 and then at x = 50 and the area under that portion of the curve is 250. How would I find the function that represents these parameters?

One arch of the sine function has intercepts at x = 0 and x = $\pi$. Two of the several kinds of transformations you can apply are compressions and expansions, which make each arch narrower or wider, respectively. The graph of y = sin(2x) represents a compression toward the y-axis of the basic, untransformed function by a factor of 2, so that the intercepts mentioned before are now at x = 0 and x = $\pi/2$.

The graph of $y = \sin(\frac 1 3 x)$ represents an expansion away from the y-axis of the untransformed function by a factor of 3. The intercepts of the transformed graph are now at x = 0 and x = $3\pi$.

I leave it to you to figure out what the multiplier needs to be so that the intercepts will be at x = 0 and x = 50.

 

[Ssnow]

Hi, if you want to fix the interval, in order to find the area equal to 250 you must change other things with constant and solve a linear equation (possibly linear), you can follow the suggestion of Mark44 and search for a function as $C\sin{\left(\frac{x\pi}{50}\right)}$ for $x\in [0,50]$, so from the condition $\int_{0}^{50}C\sin{\left(\frac{x\pi}{50}\right)}d\, x=250$ you can find $C$...

 

[Ocata]

One arch of the sine function has intercepts at x = 0 and x = $\pi$. Two of the several kinds of transformations you can apply are compressions and expansions, which make each arch narrower or wider, respectively. The graph of y = sin(2x) represents a compression toward the y-axis of the basic, untransformed function by a factor of 2, so that the intercepts mentioned before are now at x = 0 and x = $\pi/2$.

The graph of $y = \sin(\frac 1 3 x)$ represents an expansion away from the y-axis of the untransformed function by a factor of 3. The intercepts of the transformed graph are now at x = 0 and x = $3\pi$.

I leave it to you to figure out what the multiplier needs to be so that the intercepts will be at x = 0 and x = 50.

Thank you Mark44.

For x-intercept at one full arc:

$x = 50$

$(?) x = 50(?)$

$\frac{π}{50} x = 50\frac{π}{50}$

$\frac{π}{50} x = π$, then

$Sin(\frac{π}{50} x) = f(x)$or if I want to phrase the question starting in terms of the full period of the sine graph:$x = 100$

$(?)x = 100(?)$

$(\frac{π}{50})x = 100(\frac{π}{50})$

$(\frac{π}{50})x = 2π$, then

$Sin(\frac{π}{50} x) = f(x)$
This was a bit confusing at first, so it was definitely a worthwhile exercise because now, after playing with the numbers a bit, I am very comfortable with evaluating the information on the x-axis when the sine graph passes through the origin and any other x-intercept to form the terms inside the parenthesis of the sine function.

Also, I recently learned from SteamKing, in a previous thread, how the terms inside the parenthesis of a sine function translate to the Period of the sine graph, so his recent advice combined with your current advice on this new question, has greatly helped me to see the full scope of how the x-axis and the information inside the parenthesis of the sine function are related. Thank you.

 

[Ocata]

Hi, if you want to fix the interval, in order to find the area equal to 250 you must change other things with constant and solve a linear equation (possibly linear), you can follow the suggestion of Mark44 and search for a function as $C\sin{\left(\frac{x\pi}{50}\right)}$ for $x\in [0,50]$, so from the condition $\int_{0}^{50}C\sin{\left(\frac{x\pi}{50}\right)}d\, x=250$ you can find $C$...

Thus

$\int_{0}^{50}C\sin{\left(\frac{x\pi}{50}\right)}d\, x=250$

$C = 2.5π$

$\int_{0}^{50}(2.5π)\sin{\left(\frac{x\pi}{50}\right)}d\, x=250$

$f(x) = 2.5πSin(\frac{π}{50}x)$

This is the concept that jbriggs444 explained previously in this thread with regard to the parabola. Thank you, Ssnow, for your guidance on applying the scaling factor concept to the sine function.

I now understand how to find the functions for parabolas and sine curves given the area and x-intercepts of their graphs. Thank you.