Around which points to make T=I(alpha)

[Karol]

Homework Statement

I was told that I can use the rigid body angular momentum formula T=I$\alpha$
Aroud 3 points: a fixed one (I assume the temporary center of rotation), or the center of mass or a point moving parallel to the c.m.
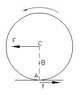
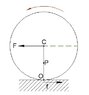
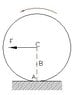
I have tested it with the case shown in the picture: a cylinder rotating on a rough surface, a steady force acting on it's center.
When calculating the angular acceleration $\alpha$ round the points A and C I get the same result, but when calculating around B-a different one, meaning the above is correct.
Why is that? the formula L=I$\omega$ is derived this way:
$$L=\sum_{n=1}^N L_n=\sum_{n=1}^N m_nv_n\cdot r_n=\sum_{n=1}^N m_nr^2_n \omega=I\omega$$
So, I understand, in order to get the velocity of the particle correct, I have to calculate only round the stationary point of rotation. The formula T=I$\alpha$ is only the derivative of the former.
Can anyone explain a bit, and give a name of a book that explains this in detail, since some ordinary books talk only in general about this.

 

[tiny-tim]

Hi Karol!

When calculating the angular acceleration $\alpha$ round the points A and C I get the same result, but when calculating around B-a different one, meaning the above is correct.

No, the velocity of B is parallel to that of the centre of mass (C), so the result should be the same.

Have you included the friction force at A (not in the diagram) … if there's no friction, then why would the angular speed change?

(and sorry, I don't know any book that goes into this )

 

[Karol]

There's friction and I included it in my calculation for point B. Around point A:

[tex]T_A=I_A\alpha[/itex]<br /> [tex]FR=(kmR^2+mR^2)\alpha\Rightarrow\alpha=\frac{F}{mR(k+1)}[/itex]<br /> <br /> I get the same $\alpha$ when I calculate round point C.<br /> What is the friction force f ?<br /> $$\sum F=ma\Rightarrow F-f=ma=mR\alpha=mR\frac{F}{mR(k+1)}$$<br /> $$\Rightarrow f=F\frac{k}{k+1}$$<br /> <br /> Around point B:<br /> <br /> [tex]T_B=I_B\alpha[/itex]<br /> <br /> $$F\frac{R}{2}+f\frac{R}{2}=(kmR^2+m\frac{R^2}{4})\alpha$$<br /> $$\Rightarrow \alpha=\frac{2F(2k+1)}{mR(k+1)(4k+1)}$$<br /> <br /> And it's not the same as the first.<br /> How do you, Tiny-Tim, know this subject with no book to offer?[/tex][/tex][/tex]

 

[tiny-tim]

Hi Karol!

Your formula τ_B = I_Bα is wrong …

The angular momentum about any point P is Iω about the centre of mass (C) plus the (ordinary) moment about B of the total momentum (mv_c.o.m.) as if it were at C.

ie L_P = I_Cω + m PC x v_c.o.m.

If P is on the axis of rotation, then v_c.o.m. = PC x ω, and so L_P = (I_C + md²)ω = I_Pω.

In any other case, L_P is not I_Pω

(and τ_P is not I_Pα)

In other words:

The parallel axis theorem (I_P = I_C + md²) is only useful at the centre of rotation* (or, if you have a body made up of parts, you can apply it at the centre of mass of the whole body for each part for which you know the moment of inertia )

* to be precise: on the axis of rotation​

 

[Karol]

I assume L_P = I_Cω + m PC x v_c.o.m. comes from the transformation of vectors between moving coordinate systems:
$\Vec{A_2}$ is vector A₂ relative to the ground
$\Vec{A_1}$ is vector A₁ relative to the ground
$\Vec{A_{21}}$ is vector A₂ relative to vector A₁
$$\Vec{A_2}=\Vec{A_1}+\Vec{A_{21}}$$
But I think you switched the places of the vectors in:
v_c.o.m. = PC x ω
It should be:
v_c.o.m. = ω x PC
Since then the direction of v_c.o.m. comes out correct.

 

[tiny-tim]

Yeah, I can never remember which way round that is !

 

[Karol]

How is this equation derived?
L_P = I_Cω + m PC x v_c.o.m.

 

[tiny-tim]

How is this equation derived?
L_P = I_Cω + m PC x v_c.o.m.

L_P = ∫∫∫ (r - r_P) x ρ v dxdydz

= ∫∫∫ (r - r_P) x ρ (ω x (r - r_c.o.m.) + v_c.o.m.) dxdydz

= ∫∫∫ (r - r_P) x ρ (ω x (r - r_c.o.m.) dxdydz + (∫∫∫ ρ (r - r_P) dxdydz) x v_c.o.m.

= ∫∫∫ (r - r_c.o.m.) x ρ (ω x (r - r_c.o.m.) dxdydz + (mv_c.o.m. - mr_P) x v_c.o.m.

(because ∫∫∫ ρ (r - r_c.o.m.) dxdydz = 0)

= I_c.o.m.ω + m PC x v_c.o.m. ​

More indirectly, but shorter (with v_P being the velocity of the part of the body at position P) …

L_P = ∫∫∫ (r - r_P) x ρ v dxdydz

= ∫∫∫ (r - r_P) x ρ (ω x (r - r_P) + v_P) dxdydz

= ∫∫∫ (r - r_P) x ρ (ω x (r - r_P)) dxdydz + (∫∫∫ ρ (r - r_P) dxdydz) x v_P

= I_Pω + m PC x v_P​

and then applying the parallel axis theorem …

= I_c.o.m.ω + m PC x v_c.o.m. ​

(and if P is the centre of rotation, so that v_P = v_c.o.r. = 0, then:

= I_c.o.r.ω)​

 

[Karol]

First, Tiny-Tim, I thank you very much. You feed my curiosity...

But I don't understand the transition between:
∫∫∫ (r - r_P) x ρ (ω x (r - r_c.o.m.) dxdydz + (∫∫∫ ρ (r - r_P) dxdydz) x v_c.o.m.
And:
∫∫∫ (r - r_c.o.m.) x ρ (ω x (r - r_c.o.m.) dxdydz + (mv_c.o.m. - mr_P) x v_c.o.m.

In the first integral, I guess you did:
r - r_P=(r_c.o.m.-r_P)+(r - r_c.o.m.)=PC+(r - r_c.o.m.)

Taking PC and returning to the integral:

∫∫∫PC x ρ (ω x (r - r_c.o.m.) dxdydz=
∫∫∫PC x ρ (ω x r - ω x r_c.o.m.) dxdydz=
∫∫∫ρ PC x (ω x r) - PC x (ω x r_c.o.m.) dxdydz

None of these yields ∫∫∫ ρ (r - r_c.o.m.) dxdydz.

In the second integral:

∫∫∫ρr_Pdxdydz=mr_P

But:

∫∫∫ρrdxdydz Is not equal to mv_c.o.m.

 

[tiny-tim]

Hi Karol!

In the second integral, you're right … I mistyped mv_c.o.m. instead of mr_c.o.m. …

the next line is correct, though, since (mr_c.o.m. - mr_P) x v_c.o.m. = m PC x v_c.o.m.

In the first integral, r_c.o.m. r_P and ω are all independent of x y and z, so they come outside the ∫∫∫, leaving only ∫∫∫ (r - r_c.o.m.) dxdydx = 0

 

[Karol]

∫∫∫ (r - r_P) x ρ (ω x (r - r_c.o.m.) dxdydz=
ρ ω x ∫∫∫ (r - r_P) x (r - r_c.o.m.) dxdydz=
ρ ω x ∫∫∫ r x (r - r_c.o.m.)dxdydz - ∫∫∫r_P x (r - r_c.o.m.)dxdydz=
ρ ω x ∫∫∫ r x (r - r_c.o.m.)dxdydz+0=
ρ ω x (∫∫∫ r x r - ∫∫∫ r x r_c.o.m.)=
ω x ∫∫∫ ρ r x r_c.o.m.

But this does not give ωI_c.o.m., or does it?

 

[tiny-tim]

∫∫∫ (r - r_P) x ρ (ω x (r - r_c.o.m.) dxdydz=
ρ ω x ∫∫∫ (r - r_P) x (r - r_c.o.m.) dxdydz=

You can't do that!

A x (B x C) is nothing like B x (A x C)

 

[Karol]

∫∫∫ (r - r_P) x ρ ω x (r - r_c.o.m.) dxdydz=
∫∫∫ r x ρ ω x (r - r_c.o.m.) - ∫∫∫ r_P x ρ ω x (r - r_c.o.m.)=
∫∫∫ r x ρ ω x (r - r_c.o.m.) - 0=
∫∫∫ r x ρ ω x r - ∫∫∫ r x ρ ω x r_c.o.m.=
∫∫∫ r x ρ ω x r - (∫∫∫ r x ρ ω) x r_c.o.m.

 

[Karol]

Please, Tiny-Tim, complete the explanation.
In my previous post I wrote the equations, but didn't get the required result: I_c$\omega$

 

[tiny-tim]

It's at the start of my post #8 …

you need to have an (r - r_c.o.m.) on the extreme left for it to work (to get I_c.o.m.) …

for some reason you decided not to do so!

 

[Karol]

But that's exactly my question!
At the extreme left on the first formula:
∫∫∫ (r - r_P) x ρ ω x (r - r_c.o.m.) dxdydz + ...
There is: (r - r_P)
But then the extreme left member changes to: (r - r_c.o.m.) in the next equation:
∫∫∫ (r - r_c.o.m.) x ρ ω x (r - r_c.o.m.) dxdydz + ...
And the rest of these two formulas is the same. how to make the transition of (r - r_P) to (r - r_c.o.m.)?

 

[tiny-tim]

how to make the transition of (r - r_P) to (r - r_c.o.m.)?

Because …

(because ∫∫∫ ρ (r - r_c.o.m.) dxdydz = 0)

… (and r_P is constant).

 

[Karol]

I now understand I shouldn't open the parentheses. I understand that From your second example with v_P.
But in your first analysis I don't understand how you got the same member twice, as needed and as described in your second example.
That is, from:
∫∫∫ (r - r_P) x ρ ω x (r - r_c.o.m.) dxdydz + ...
There is: (r - r_P)
But then the extreme left member changes to: (r - r_c.o.m.) in:
∫∫∫ (r - r_c.o.m.) x ρ ω x (r - r_c.o.m.) dxdydz + ...
how to make the transition of (r - r_P) to (r - r_c.o.m.)?
And you write that

(because ∫∫∫ ρ (r - r_c.o.m.) dxdydz = 0)

Where do you get this without opening parentheses?

 

[tiny-tim]

it's the definition of the centre of mass

 

[Karol]

I know the definition of C.M.. I ask how, in what way, you arrived to the partial expression:
∫∫∫ ρ (r - r_c.o.m.) dxdydz
From the formula:
∫∫∫ (r - r_P) x ρ ω x (r - r_c.o.m.) dxdydz

But my main question is this:
You have changed the first member, (r - r_P), in the formula:
∫∫∫ (r - r_P) x ρ ω x (r - r_c.o.m.) dxdydz
To (r - r_c.o.m.) In the formula:
∫∫∫ (r - r_c.o.m.) x ρ ω x (r - r_c.o.m.) dxdydz
By what right? what's the process you have made for that.
From there, I guess, I'll go on my own.
Thanks.

 

[tiny-tim]

You have changed the first member, (r - r_P), in the formula:
∫∫∫ (r - r_P) x ρ ω x (r - r_c.o.m.) dxdydz
To (r - r_c.o.m.) In the formula:
∫∫∫ (r - r_c.o.m.) x ρ ω x (r - r_c.o.m.) dxdydz

Because I subtracted ∫∫∫ (r_P - r_c.o.m.) x ρ ω x (r - r_c.o.m.) dxdydz,

which is a constant "times" ∫∫∫ ρ (r - r_c.o.m.) dxdydz, which = 0.

 

[Karol]

Thank you very much, Tiny-Tim. It's a relief.

I think you should add ∫∫∫ (r_P - r_c.o.m.) x ρ ω x (r - r_c.o.m.) dxdydz, instead of subtracting, since then you get ∫∫∫ (r - r_c.o.m.) x ρ ω x (r + r_c.o.m.) dxdydz.

 

[Karol]

I try to calculate $\alpha$ around point P, as drawn.
I don't get the right answer, since I get a different $\alpha$ at points O and C, which is (round point O):
$$M_O=I_O\alpha\Rightarrow FR=(KmR^2+mR^2)\alpha<br /> \Rightarrow \alpha=\frac{F}{mR(K+1)}$$

I take the derivative of L_P = I_Cω + m PC x v_c.o.m. and get M_P = I_Cα + m PC x a_c.o.m..

I find the friction force, with the help of $\alpha$:
$$\Sigma F=ma \Rightarrow f=F\frac{K}{K+1}$$

M_P = I_Cα + m PC x a_c.o.m.

$$\Rightarrow\left(F\frac{R}{2}\cdot f \frac{R}{2}\right)\hat{z}=mR^2\left(K+\frac{1}{4}\right)\vec{\alpha}+\left(m\frac{R}{2}\cdot\frac{F}{m(K+1)}\right)\hat{z}$$
$$\alpha=\frac{4FK}{mR(K+1)(4K+1)}$$

Which is not the same as the previous I found.

 

[tiny-tim]

Hi Karol!

The dot should be a +, and the "+ 1/4" shouldn't be there.

Then your equation becomes

(2K+1)R/2(K+1) = (Rα/a)2KR/2(K+1) + R/2(K+1)

 

[Karol]

The "+ 1/4" should be there since point P is on the half of the radius.
And there is no F in your equation.

 

[tiny-tim]

The (K + 1/4) is supposed to be part of I_C not I_P, so the "+ 1/4" shouldn't be there

(I canceled the Fs … ok?)

 

[Karol]

You cannot cancel the Fs, it doesn't appear in the α member:
$$\left(F\frac{R}{2}+f \frac{R}{2}\right)\hat{z}=KmR^2\vec{\alpha}+\left(\frac{R}{2}\cdot\frac{RF}{m(K+1)}\right)\hat{z}$$

 

[tiny-tim]

oh, that (Rα/a) shouldn't be there …
(2K+1)R/2(K+1) = (Rα/a)2KR/2(K+1) + R/2(K+1)

that should have been …
(2K+1)R/2(K+1) = 2KR/2(K+1) + R/2(K+1)

(using α = F/MR(K+1))

 

[Karol]

that should have been …
(2K+1)R/2(K+1) = 2KR/2(K+1) + R/2(K+1)
(using α = F/MR(K+1))

First, you can't use α = F/MR(K+1) since I have to find α.
Second, your last m PC x a_c.o.m. member, R/2(K+1), is not correct.
It should be:
$$\left( \frac{R}{2}\cdot\frac{RF}{m(K+1)}\right)$$
Which gives FR²/2M(K+1)

 

[tiny-tim]

First, you can't use α = F/MR(K+1) since I have to find α.

Yes, I can … you found α from calculations based on the centre of mass.

All I had to do was show that that was consistent.

Second, your last m PC x a_c.o.m. member, R/2(K+1), is not correct.

Yes it is, it's exactly the same as yours, except for a factor of RF/M which I took out from the whole equation.