AS Physics Basic Kinematics Question

[seiei]

Homework Statement

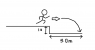
A sprinter moving horizontally takes off from a point 1.0m above the ground and lands 3.0m away. Calculate how fast the sprinter is running.

Homework Equations

Attempted using SUVAT equations but too many unknowns (acceleration and time of travel) to figure out the initial speed.

The Attempt at a Solution

Tried using SUVAT equation as mentioned above but to no avail. Also mgh=½mv² but I think that only works when the object is falling in a straight line and not falling in a curved manner. Any help would be much appreciated. Thank you :)

 

[seiei]

Here's a rough picture of the problem in case I'm not being specific enough

 

[Hootenanny]

The trick in these types of questions, is consider the two components (horizontal and vertical) of motion separately and apply the SUVAT equations independently to each component.

 

[seiei]

In this case could I use s=vt+½at² where the final velocity=0m/s, acceleration is gravitational force= 9.81m/s² and distance s= 3m?

 

[Hootenanny]

In this case could I use s=vt+½at² where the final velocity=0m/s, acceleration is gravitational force= 9.81m/s² and distance s= 3m?

Careful! The final velocity is not zero. Think of when you drop an object vertically from height, its velocity just at the point of impact is non-zero.

 

[seiei]

Okay I'm feeling a bit lost now... If the final velocity is another unknown, how am I meant to resolve the vertical component?

 

[Hootenanny]

Okay I'm feeling a bit lost now... If the final velocity is another unknown, how am I meant to resolve the vertical component?

What do you know about the vertical component?

 

[seiei]

There is a height of 1.0m and an acceleration of 9.81m/s²

 

[Hootenanny]

There is a height of 1.0m and an acceleration of 9.81m/s²

What about the initial velocity in the vertical direction? And the final height?

 

[seiei]

Isn't the initial velocity the thing I'm trying to figure out? Or is that zero? And the final height is zero (?)

 

[Hootenanny]

Isn't the initial velocity the thing I'm trying to figure out? Or is that zero? And the final height is zero (?)

You want to calculate the initial horizontal velocity. If the runner is initially moving horizontally, what is his initial vertical velocity?

 

[seiei]

Zero? I'm not entirely sure. Sorry bout this ><

 

[Hootenanny]

Zero? I'm not entirely sure. Sorry bout this ><

Yes. So you now know the initial vertical velocity, the initial and final heights and the acceleration.

Now, what do you need to know in order to work out how fast the runner took off?

 

[seiei]

The time it takes for the runner to reach the ground? (sorry I have to go to bed now, GMT+12 makes it nearly quarter to 11 at night) Hopefully we can resume this tomorrow. Thank you for your time! :)

 

[Hootenanny]

The time it takes for the runner to reach the ground? (sorry I have to go to bed now, GMT+12 makes it nearly quarter to 11 at night) Hopefully we can resume this tomorrow. Thank you for your time! :)

Correct! And you can get that from the vertical motion problem.

No problem and no need to apologise. These problems can seem confusing on the first attack.

 

[seiei]

So to find the time it takes for the runner to reach the ground is represented by s=ut+½at² where the initial vertical velocity= 0. Rearranging the equation makes t= 0.45s when a=9.81m/s². Then resolving the horizontal component using the same equation s=ut+½at² a= 0 meaning that u=3÷0.45= 6.64m/s. Is this right?

 

[Hootenanny]

So to find the time it takes for the runner to reach the ground is represented by s=ut+½at² where the initial vertical velocity= 0. Rearranging the equation makes t= 0.45s when a=9.81m/s². Then resolving the horizontal component using the same equation s=ut+½at² a= 0 meaning that u=3÷0.45= 6.64m/s. Is this right?

You are indeed, correct.

 

[seiei]

Yuss! Thanks for your help Hootenanny! :D

 

[PeterO]

So to find the time it takes for the runner to reach the ground is represented by s=ut+½at² where the initial vertical velocity= 0. Rearranging the equation makes t= 0.45s when a=9.81m/s². Then resolving the horizontal component using the same equation s=ut+½at² a= 0 meaning that u=3÷0.45= 6.64m/s. Is this right?

Those figures seem OK.

Remember, the only quantity that is common to the vertical motion calculations and the horizontal calculations is time. and if you need the time to calculate something in the horizontal part, it can almost certainly be calculated from the vertical considerations, and vice versa.