Astrophysics: Parallax method

[kingwinner]

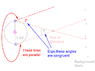
1) From the ground of the Earth, atmospheric turbulence limits the typical best image to a full-wide-at-half-maximum (FWHM) of ~0.5 arcsceond (this is an angle). Suppose we can determine positional accuracy of stars to ~1/10 of the FWHM, to how far in light years can we use the parallax method to measure the distance to stars?

Now I am stuck on this question. My biggest trouble is that I don't know how to relate the 0.5 arcsceond to the parallax method or parallax angle. Can someone please help me out?

Any help is greatly appreciated!

 

[kingwinner]

Big test tomorrow...and this is a typical problem...
Can someone please help me?

 

[jeroen]

Measuring a star's distance by parallax basically is solving a triangle:
The base and the two angles at the base are known and the height of the triangle needs to be calculated.

However, the angles aren't known exactly, there is a certain error.
So a measured angle of 60 degrees might actually be anything between 55 and 65 degrees.

Draw this situation on paper (two lines going out from each observation point) and you will see that the star will be somewhere inside a stretched diamond made up of the lines from the observation points.

How will the distance of the star, the length of the base and the size of the error affect the shape of this diamond?

 

[kingwinner]

You said that for the parallax method, we need two angles...

But there is only one angle (0.5 arcsceond) given in this problem...I am very confused...

 

[hage567]

You don't need two angles for this. If you don't know the formula, it can be worked out by trig if you draw a diagram. Once you do that, you will have the relationship between the distance and the angle. Then you can work out how far you can measure based on the angle info given to you in your problem.

 

[kingwinner]

I don't get the setup of the problem!

For example, in a diagram like this, WHERE exactly is the angle being referred as 0.5 arcsecond?
http://www.geocities.com/paulntobin/image/parallax.gif

 

[DaveC426913]

The angle is the difference between the apparent positions in the sky from the observer's location (i.e. the star is at 43:00'10.0" vs. 43:00'10.5"). This is what you've illustrated in the two insets in your diagram.

The key is this:

that angle can be shown to be equal to the angle you have in your main diagram labelled "Nearby star "N"". And THIS is the triangle you are solving.

(Sorry if this arrived late. Hope you did well.)

 

[kingwinner]

The parallax angle is labelled "p" in the above figure.

When we talk about distance to galaxies or stars, is it the distance measured from the Sun or is it the distance from the Earth?


"that angle can be shown to be equal to the angle you have in your main diagram labelled "Nearby star "N" " <----can you please explain why there are equal?

Is the answer to question 1: d=(1/0.025) pc ??

 

[DaveC426913]

When we talk about distance to galaxies or stars, is it the distance measured from the Sun or is it the distance from the Earth?

Being that a parsec is about 4.3 light YEARS, and the Earth Sun difference is at worst 8 light MINUTES (and at best 0*), the difference between Earth distance and Sun distance is about 0.0004% of your answer - that's 4 parts in one million.

*The differences in distance depend on whether we are viewing perpendiculur or parallel to the plane of Earth's orbit. If perpendicular, the Earth and Sun are the same distance from the star.

 

[DaveC426913]

"that angle can be shown to be equal to the angle you have in your main diagram labelled "Nearby star "N" " <----can you please explain why there are equal?

According to the http://library.thinkquest.org/20991/geo/parallel.html" of parallel lines and transverse lines. Look at angles labelled 3 and 5.

Compare to attached diagram.

 

[kingwinner]

Oh, I see! Thanks!

Is the answer to question 1: d=(1/0.025) pc ? (becaue the 0.5arcseconds is the subtended angle of the apparent positions of the star and the parallax angle is 1/2 of it...?) I am just trying to make sure I am understanding this correctly...


Also, I have another question. How come we are unable to use the parallax method to measure the distance to stars when the full-wide-at-half-maximum is less than 0.5 x 1/10 = 0.05 arcseconds? I just don't get why...

Thanks for helping me!

 

[DaveC426913]

I'm no help there. Sorry.

 

[kingwinner]

Is the answer to question 1: d=(1/0.025) pc ? (becaue the 0.5arcseconds is the subtended angle of the apparent positions of the star and the parallax angle is 1/2 of it...?) I am just trying to make sure I am understanding this correctly...


Also, I have another question. How come we are unable to use the parallax method to measure the distance to stars when the full-wide-at-half-maximum is less than 0.5 x 1/10 = 0.05 arcseconds? I just don't get why...

Thanks for helping me!

Does anyone have any idea?

 

[DaveC426913]

Well, I would guess that the reason you can't go much lower than .5 arcsecond is because the margin or error increases dramatically as the angle gets smaller. I imagine .5 arcsecond is an arbitrary limt.