Average power of a signal in spectral display

[axcelenator]

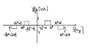
Hello, I've got a modulated signal - Y(f) (the question doesn't say if AM or DSB or whatever) which it's spectral modulted signal is shown(in the file I've uploaded).its is modulated by a carrier of sum of several COS.

It asks what is the average energy or power( I should decide) of the modulated signal y(t)^2 - if W=100kHZ.


I think that it is power signal.
I've tried to do that with parseval:∫|Y(f)|df from and got 400KJoule. but I don't know wheter it right or wrong and I don't know how to do the Integral because it is not periodic.
Thanks!

 

[rude man]

I am a bit confused that Y is expressed in volts. I think it should be V/root Hz or V^2/Hz since there is clearly a continuum of frequencies in a bandwidth of W. If it were V then there would be an infinity of spot frequencies in a bandwidth W with attendand infinite power.

So unless you get better info I would consider the y-axis as V/root Hz, then you can easily determine the total power by looking at the +x axis spectral distributions.

 

[marcusl]

In addition to the erroneous units that rude man pointed out, please note that 1) Parseval's theorem gives you energy, not power, and 2) your integral must be modified to be correct.