- #1
jtmbii
- 3
- 0
I've been studying this problem, trying to understand the given answer, but still no success.
<<provided in attachment>>
Longitudinal Strain

Latitudinal Strain:
 where
where
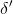 is the amount the radius contracts, r is original radius
is the amount the radius contracts, r is original radius
Average Normal Stress:
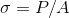
Poisson's Ratio (Longitudinal Strain & Lateral Strain):
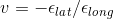
Hooke's Law (Stress & Strain):
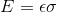
Elastic Deformation of an Axially Loaded Member w/ a constant load & cross-sectional area:
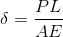
(My equations are according to Hibbeler's Mechanics of Materials 8th ed.)
This problem was given after studying axial loads. Though it seems that this problem encorporates everything we have learned in the class so far. The way I would have done this problem is to just find the deformation (delta). Subtract the deformatin from "L" to get an new "L" value and then try to find the change in diameter from there by knowing the formula for area of the cross section. But I must not understand the concept at all because the solution shows that's not the approach at all. I did not think Stress & Strain was something I had to calculate.
The following is my attempt to understand the steps:
Looking at the solution, I'm not sure what the 0.35 is. Or why it is calculated. I thought it was
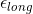 at first. But when I calculate
at first. But when I calculate
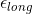 using the eqn above I cannot get 0.35. Or it might be the dividend of (diameter/length) but then that means there is a power of 10 error. The next part is calculated stress then strain using Hooke's Law. Then the solution uses Poisson's Ratio to find
using the eqn above I cannot get 0.35. Or it might be the dividend of (diameter/length) but then that means there is a power of 10 error. The next part is calculated stress then strain using Hooke's Law. Then the solution uses Poisson's Ratio to find
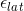 with the 0.35 earlier which I assume is
with the 0.35 earlier which I assume is
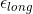 . Then by using the strain in the lattitude direction we can find the reduction of the diameter.
. Then by using the strain in the lattitude direction we can find the reduction of the diameter.
Short version/Main questions: What is the 0.35? How was 0.35 calculated? Why the original method I thought of does not apply here? Why does the method in the solution work?
I appreciate the help. Thank you.
Homework Statement
<<provided in attachment>>
Homework Equations
Longitudinal Strain
Latitudinal Strain:
Average Normal Stress:
Poisson's Ratio (Longitudinal Strain & Lateral Strain):
Hooke's Law (Stress & Strain):
Elastic Deformation of an Axially Loaded Member w/ a constant load & cross-sectional area:
(My equations are according to Hibbeler's Mechanics of Materials 8th ed.)
The Attempt at a Solution
This problem was given after studying axial loads. Though it seems that this problem encorporates everything we have learned in the class so far. The way I would have done this problem is to just find the deformation (delta). Subtract the deformatin from "L" to get an new "L" value and then try to find the change in diameter from there by knowing the formula for area of the cross section. But I must not understand the concept at all because the solution shows that's not the approach at all. I did not think Stress & Strain was something I had to calculate.
The following is my attempt to understand the steps:
Looking at the solution, I'm not sure what the 0.35 is. Or why it is calculated. I thought it was
Short version/Main questions: What is the 0.35? How was 0.35 calculated? Why the original method I thought of does not apply here? Why does the method in the solution work?
I appreciate the help. Thank you.
