Calculate deflection of rod/axlepipe due to distributed load

[Krismein]

Summary:: Calculate the deformation on a rod/axle/pipe due to a distributed load.

I’m manually trying to calculate the deformation on a rod/axle/pipe due to a distributed load. The rod has an outer diameter of 62mm and an inner diameter of 50, is 170mm long, made from a material with an E-module=200GPa and Poisson's ratio = 0,3. The load is distributed along the whole length of the rod and is 491 N/mm. I have calculated the second moment of inertia I to be 418536mm^4, and I’m having no luck finding a formula for rod deformation/bending.

I have tried using this formula:

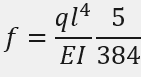
But i don't think it applies for rods, as my answer is low.

 

[berkeman]

Is this question for your work or is it a schoolwork question?

 

[Lnewqban]

Where did you get that equation from?
The type of support is very important.

 

[Krismein]

Where did you get that equation from?
The type of support is very important.

From a Norwegian book for engineering. Posting a pic below.

 

[Krismein]

Is this question for your work or is it a schoolwork question?

For my bachelor thesis

 

[berkeman]

Nice. I'll move it to the schoolwork forums then.