B field intensity of 2 parallel wires

[arl146]

Homework Statement

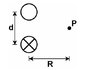
Two long parallel wires are a center-to-center distance of 4.60 cm apart and carry equal anti-parallel currents of 4.40 A. Find the magnetic field intensity at the point P which is equidistant from the wires. (R = 4.00 cm).

Homework Equations

magnetic field for a long straight wire = μi/2*pi*r

The Attempt at a Solution

at first i thought it was just 0 T since the current is in opposite directions but that was wrong. so i worked it out and saw that the y components cancel out and you're left with the 2 x directions components. so i thought B = $\frac{2*μ*i*cos(theta)}{2*pi*r}$

where cos(theta) = R/r
where r = sqrt(R²+(d/2)²)

this didnt work out for me. my answer was 7.1665340225x10^(-4) T and it said it was wrong

B= $\frac{2*4*pi*10^-7*4.4*.04}{2*pi*(R^2+(d/2)^2)^(3/2)}$

anything i did wrong, plugged in wrong numbers or what?

 

[Redbelly98]

I see two problems:

1. I don't see where the "3/2" exponent comes from in your denominator, the units do not work out properly with that exponent there.

2. It appears you made an arithmetic mistake in evaluating your expression -- I get a different number for the expression you wrote, but as I indicated I don't think the 3/2 exponent there is correct anyway.