Electro
- 48
- 0
Hello Everyone,
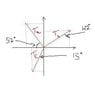
I solved an exercise that has to do with equilibrium. There are 3 forces and I should find the tensions Ta and Tb in the 2 cords. (I drew a simple picture so that it would be more clear to you). I solved the exercise following physical principles (I think I did it correct) but I get negative values for Ta and Tb.
The equations I derived are:
Tb*sin(42) - Ta*cos(57)-Tc*sin(15)=0 For X
Tb*cos(42)+Ta*sin(57)-Tc*cos(15)=0 For Y
But still I get the negative values. What might be wrong?
I solved an exercise that has to do with equilibrium. There are 3 forces and I should find the tensions Ta and Tb in the 2 cords. (I drew a simple picture so that it would be more clear to you). I solved the exercise following physical principles (I think I did it correct) but I get negative values for Ta and Tb.
The equations I derived are:
Tb*sin(42) - Ta*cos(57)-Tc*sin(15)=0 For X
Tb*cos(42)+Ta*sin(57)-Tc*cos(15)=0 For Y
But still I get the negative values. What might be wrong?