chris61986
- 8
- 1
Well, I took my Physics final today, and I passed it but I didn't do quite as well as I'd hoped. Anyway, there was one problem I spent tons of time trying to figure out. I've tried giving it a shot again at home, but it's still eluding me. Some guidance would be great! Sorry if this is vague, but I'm writing this from memory.
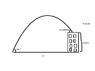
A ball is thrown from the ground and after 4 seconds lands on top of a building 20m high. When it lands, it is at an angle of 60°. Find the distance traveled and the angle from the ground with respect to the x-axis.
Known:
Landing Angle, θ=60°
Time = 4s
Height of building = 20m
And my crude drawing is attached.
KE and PE
Kinematics
I'm not trying to solve at this point, I just want to be able to find the first unknown.
So I've tried everything I can think of to try. I was leaning toward using PE at the top of the curve to equal KE right before it hits. I'll call H the max height and h the height of the building. This would leave me with mgH = 1/2mv^2*sin(θ) + mgh
From here, I have two unknowns. The final velocity and the maximum height, and it just seems like no matter what other equations I use, I still have two unknowns. Can someone give me a hint?
Homework Statement
A ball is thrown from the ground and after 4 seconds lands on top of a building 20m high. When it lands, it is at an angle of 60°. Find the distance traveled and the angle from the ground with respect to the x-axis.
Known:
Landing Angle, θ=60°
Time = 4s
Height of building = 20m
And my crude drawing is attached.
Homework Equations
KE and PE
Kinematics
The Attempt at a Solution
I'm not trying to solve at this point, I just want to be able to find the first unknown.
So I've tried everything I can think of to try. I was leaning toward using PE at the top of the curve to equal KE right before it hits. I'll call H the max height and h the height of the building. This would leave me with mgH = 1/2mv^2*sin(θ) + mgh
From here, I have two unknowns. The final velocity and the maximum height, and it just seems like no matter what other equations I use, I still have two unknowns. Can someone give me a hint?