Ball rolling down a surface - where is the axis of rotation?

[lillybeans]

In my textbook, it says that when a ball rolls down a surface, inclined or not, the point of contact can be thought of as the pivot or the axis of rotation, since at the point of contact, the ball's velocity is zero. Makes sense, but then the textbook becomes inconsistent in problems solving.

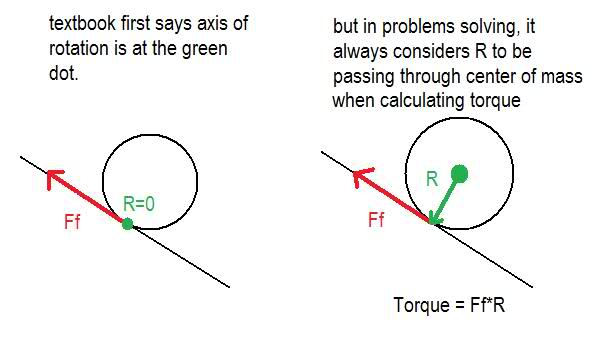
There are a few exercises of spheres rolling down surfaces, both inclined and non-inclined. If the point of contact between the ball and the surface is the axis of rotation, then the torque done by friction would be zero because it passes through the axis of rotation! In other words, it acts AT the pivot, the point of contact. But in the solutions, they clearly say the torque done by friction is "fR, where R is the radius of the ball". But aren't they now REDEFINING the axis to be the center of mass, hence the "R"?

I guess gravity is not affected by the axis of rotation in either of these cases cause it always passes through the axes of rotation in both cases. But friction is.

Can anyone explain the discrepancy? Thank you in advance!

 

[LawrenceC]

The point of contact is called the instantaneous center. The torque is not zero because the force (mg) does not pass through it.

 

[Khashishi]

Axis of rotation is wherever you define it to be. This sets up your frame of reference. It doesn't change anything physically. Torque also depends on your choice of center.