NathanLeduc1
- 36
- 0
Homework Statement
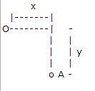
A ball of mass m is attached via a rod of length x to an axle that rotates with angular velocity ω. You can consider the ball to be a point mass.
m = 5 kg, x = 0.3 m, y = 0.4 m, ω= 30 rad/s
(a) What is the linear momentum (direction and magnitude) of the ball?
(b) What is the angular momentum (direction and magnitude) of the ball about point A?
I've included a diagram I made.The top ball has mass m = 5 kg and the bottom ball A is rotating with angular velocity ω. Hopefully that diagram makes sense...
Homework Equations
I = mr2
L=Iω
p=mv
v=rω
The Attempt at a Solution
(a) p=mv
v=rω=0.3m*30rad/s=9m/s
p=5kg*9m/s=45kgm/s clockwise
(b) L=Iω
L=mr2ω
This is where I am confused. It would be easy to calculate if A wasn't rotating but how do I . calculate the angular momentum of the ball about point A given the fact that A is rotating?