Ball Shot Up Ramp: Magnitude of Displacement

[B-80]

In Fig. 4-11, a ball is launched with a velocity of 8.50 m/s, at an angle of 50° to the horizontal. The launch point is at the base of a ramp of horizontal length d1 = 4.90 m and height d2 = 3.60 m. A plateau is located at the top of the ramp.


Fig. 4-11

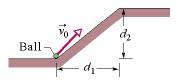
What is the magnitude of its displacement from the launch point when it lands?

The problem I am having is understanding where it lands I know that the ball is on the ramp when it is 36.3 degrees from the starting point after finding the angle of the ramp, but what is the equation to get this?

 

[mgb_phys]

Ignore the ramp for now.
What is the horizontal and vertical component of the velocity.
Now picture it thrown vertically upwards with the vertical component of the velocity, What is the time taken to reach it's maximum height ( hint v^2=u^2+2as)
Now using this time what is the horizontal distance it will have travelled.

The tricky bit it that since it is falling back onto a raised level the total time taken isn't simply twice the time to reach the top of it's path - because it doesn't have to fall all the way back to the ground.
You have to work out how long it would take to get to the top of the curve and how high this is, so you can work out the time taken to fall from the top back down to the level of the platuea.
When you have the new horizontal distance for this time you can get the distance back to the start ( hint pythagorus)

 

[mossfan563]

I'm confused on this problem. I have a similar one. How do you find t to get the vertical component?

 

[mgb_phys]

I'm confused on this problem. I have a similar one. How do you find t to get the vertical component?

Not sure what you mean 'find t ',
If you throw something upwards it slows down at a constant rate 'g' due to gravity.
The equation for the distance is s = ut + 1/2 at^2
Where u is the initial velocity, you have to be a little carefull with signs, here g is negative since it is slowing the object down. Then this equation will tell you the height at each time by just knowing the initial speed.
You can also rearrange this to get v^2 = u^2 + 2as, which since you know that v (the final velocity) is zero at the top top of the flight - when the ball momentarialy stops before falling back, you can use to get the total height 's'