Bandpass Analysis: Plot Output Voltage for R1=100Ω, R2=3kΩ, C1=100pF, C2=139nF

[Mr.Tibbs]

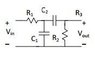
For the circuit shown below with R1 = 100 Ω, R2 = 3 kΩ, C1
= 100 pF and C2 = 139 nF, plot the output voltage as a function of time for 2 cycles
when the input voltage is vin(t) = 5V+1Vsin(2$\pi$ft) where (a) f=1 Hz and (b) f=1 MHz



2. Homework Equations

voltage divider:

$\frac{R_{2}}{R_{1}+R_{2}}$


3. Attempt
It's been a while since I've done this so this is what I have.

To solve for the voltage across capacitor one first I used a voltage divider:

v$_{1}$ = $\frac{1}{1+j\omega R_{1}C_{1}}$ = 1-6.283E-8j

I then rinse and repeated for the output.

v$_{out}$ = v$_{1}$ $\frac{j\omega R_{2}C_{2}}{1+j\omega R_{2}C_{2}}$ = 6.86498E-6+j2.62E-3

after this I'm lost because I don't even know if my output is correct. I understand that there can be a real component at low frequencies but I don't think my answer is correct to begin with. . .

 

[gneill]

Since the question is asking for a plot of the time domain response (over two cycles of input), it looks like you'll be needing to solve the differential equation for the output voltage. You could use KVL and/or KCL equations to solve for it, or perhaps go the Laplace transform route. Question: Is the 5V offset of Vin meant to be "switched on" at t = 0, or is it assumed to be present for all t < 0? Usually a source that turns on at t = 0 has the form 5V*u(t), where u(t) is the unit step function.

You can combine the transfer functions of successive circuit stages by multiplying them only if the input impedance of the subsequent stage is at least 10x that of the output impedance of the previous stage. Otherwise the two stages will interact significantly, skewing the corner frequencies and amplitudes. So check the impedances before proceeding. Otherwise you will have to perform the usual circuit analysis (KVL, KCL, esh, nodal,... whatever method you prefer).

 

[Mr.Tibbs]

The 5V exists for all of t. I know you can disregard this due to the DC behavior of the circuit, i.e. the capacitors behaving like open circuits when fully charged. Can I disregard the real portion of my answer, assuming it's just transient noise?

 

[gneill]

The 5V exists for all of t. I know you can disregard this due to the DC behavior of the circuit, i.e. the capacitors behaving like open circuits when fully charged. Can I disregard the real portion of my answer, assuming it's just transient noise?

The transient stuff is what will make the result "interesting". Consider that the network will produce a phase shift that varies with frequency. The steady-state response will just be a scaled and shifted sine wave, but what happens during the settling time?

I think the result should be interesting, particularly for the lower driving frequency...

 

[rude man]

As gneill says, it is not clear whether the sine input is followed by the unit step function U(t). If not, then the sine voltage is there for all time just as the 5V dc is, and the problem is much simpler than if there is a U(t) appended to the sine input.
.

 

[gneill]

As gneill says, it is not clear whether the sine input is followed by the unit step function U(t). If not, then the sine voltage is there for all time just as the 5V dc is, and the problem is much simpler than if there is a U(t) appended to the sine input.
.

Good catch! For some reason I was thinking that the sine component was meant to begin at t = 0 (otherwise the problem is not quite so interesting...). But you're right, the way it's presented in the problem statement it should also be considered "eternal". Perhaps Mr. Tibbs can confirm the precise text of the original problem?