MPat
- 15
- 1
Homework Statement
If a curve with a radius of 88m is perfectly banked for a car traveling at 75km/h, what must be the coefficient of static friction for a car not to skid when traveling at 95 km/hr
75km/h = 20.8m/s
95km/h = 26.4m/s
Homework Equations
Fr=mv^2/r
Fr=centripetal force
m = mass
r = radius
v = velocity
Fn= normal force
Ffr= force of friction (Us*Fn)
g = gravitational acceleration
Us = coefficient of static friction
The Attempt at a Solution
Horizontal component
sinθFn=mv^2/r Eq 1
Vertical component
cosθFn=mg
Fn=mg/cosθ Eq 2
Sub eq 2 into 1
sinθ (mg/cosθ) = mv^2/r (sinθ/cosθ = tanθ)
tanθ mg = mv^2/r
m cancels out
tanθ = v^2/gr
θ = arctan 20.8^2/9.8*88
θ = 26.6 degrees
Am I right up to there?
Now for the second part of the question. Solving for Us.
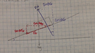
See diagram for force of friction and horizontal and vertical components
Vertical component
cosθFn - sinθFfr - mg = 0 ( there is no vertical displacement)
Solve for Fn
Fn= (sinθFfr + mg)/cosθ
Horizontal component
sinθFn + cosθFfr = mv^2/r
Sub Fn from above
sinθ ((sinθFfr + mg)/cosθ) + cosθFfr = mv^2/r
From here I am unable to isolate Ffr, or cancel out the mass... Help!
Attachments
Last edited: