Basic problem involving forces (Kleppner/Kolenkow)

[AspiringPhysicist12]

Homework Statement

In a concrete mixer, cement, gravel, and water are mixed by tumbling action in a slowly rotating drum. If the drum spins too fast, the ingredients stick to the drum wall instead of mixing.
Assume that the drum of a mixer has radius R = 0.5 m and that
it is mounted with its axle horizontal. What is the fastest the drum
can rotate without the ingredients sticking to the wall all the time?
Assume g = 9.8 m/s2.

Relevant Equations

Fn - Fc = 0
Fgcosθ - Fc=0 for object to stick to drum wall during circular motion

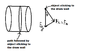
I attached my diagram/work done so far. I believe that as long as the angular velocity is always less than sqrt(2g), the object must fall downwards when it reaches the top of the drum wall. Also, the angular velocity cannot be greater than sqrt(2g), as ω=sqrt((g/r)cosθ) at all times, and can only have cosθ=1 at most. Therefore, we must have that ω<sqrt(2g) at all times to ensure the ingredient does not stick to the drum wall at all times.

My confusion is that in the answer key, it says ω ≤ sqrt(2g) rather than ω<sqrt(2g). I don't understand this because ω=sqrt(2g) is the angular velocity required for the ingredient to stick to the top of the drum wall. So if ω=sqrt(2g), the ingredient does not fall down after reaching the top of the drum wall, and the ingredient will thus will always stick to the wall. I would appreciate if it could be explained why the answer is ω ≤ sqrt(2g) rather than ω<sqrt(2g).

 

[PeroK]

I don't think you are expected to worry about whether the maximum value is included or excluded.

 

[AspiringPhysicist12]

The thing is that if I can have ω=sqrt(2g), then that means at the top of the drum wall, Fc - Fgcosθ = 0 is satisfied (which would imply that the object sticks to the wall at the top and does not fall back down). If I exclude the possibility that ω=sqrt(2g), then that means Fc - Fgcosθ is not equal to 0 at the top of the drum wall, and the object must thus fall down. That's why I think the difference between ω ≤ sqrt(2g) and ω<sqrt(2g) is significant.

 

[PeroK]

The thing is that if I can have ω=sqrt(2g), then that means at the top of the drum wall, Fc - Fgcosθ = 0 is satisfied (which would imply that the object sticks to the wall at the top and does not fall back down). If I exclude the possibility that ω=sqrt(2g), then that means Fc - Fgcosθ is not equal to 0 at the top of the drum wall, and the object must thus fall down. That's why I think the difference between ω ≤ sqrt(2g) and ω<sqrt(2g) is significant.

You'll have to write to Kleppner and Kolenkow about it!

Seriously, you got the right answer. Time to move on.

 

[AspiringPhysicist12]

Alright, thanks! I'll just move on to the next question then.

 

[hutchphd]

If I exclude the possibility that ω=sqrt(2g), then that means Fc - Fgcosθ is not equal to 0 at the top of the drum wall, and the object must thus fall down.

Just a small sanity check here: there is nothing apocalyptic that happens when there is just a little downward contact force instead of zero or upward. The cement will not "fall down"...it will just lift from the surface slightly before recontacting on the other side of the apex. So it is a continuum of results and not useful to worry about.

 

[kuruman]

Other considerations that justify not having to worry about the $\leq$ sign are: (a) the concrete lumps are not point masses and their center of mass describes a circle of smaller radius than 0.5 m; (b) concrete that is being mixed tends to be sticky which means that there are additional forces involved. This kind of physical situation works better in the clothes dryer version. As others have already said, time to move on.