What factors affect the motion of a bead on a spinning hoop?

[zaper]

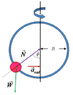
A bead of mass m can slide on a frictionless circular hoop in the vertical plane with radius R. When the hoop spins around the vertical axis with a rate of ω, the bead moves up the hoop by an angle θ which depends on the angular velocity of the hoop. (Pic attached)

a) Find θ in terms of ω, R, m and g.

b) If there is friction between the bead and hoop given by μ, within what range can ω change without changing θ?

For part a what I have so far is that a_rad=R*ω². The centripetal force (F) then is m*a_rad and the normal force is F/sinθ.

The weight needs to cancel out the normal force then so the weight in the direction of the normal force is mg*cosθ = F/sinθ

Am I anywhere close to being right?

 

[tiny-tim]

hi zaper!

no

keep it simple

do F = ma vertically to find N

then do F= ma horizontally to find ω

(and remember that the centripetal acceleration is horizontal, so use the correct r )

 

[zaper]

Hey there tiny tim!

Sorry, but I'm really struggling to keep up with this problem so forgive me for anything dumb that I do here.

So you said to find N as F=ma vertically so that means that N=mg*cosθ

By you're second part are you saying m*a_rad=m*ω²*r (r being R*sinθ)

 

[tiny-tim]

hey there zaper!

So you said to find N as F=ma vertically so that means that N=mg*cosθ

that's not in the vertical direction, is it?

By your second part are you saying m*a_rad=m*ω²*r (r being R*sinθ)

no, that's ma = ma, you need F = ma

 

[zaper]

Ok so then N=mg*sinθ I assume. Could you please explain why this is and what exactly you want for the second equation. I'm not really following you here.

 

[tiny-tim]

Ok so then N=mg*sinθ I assume.

no

start again …

F_x = ma_x

F_y = ma_y

what are a_x and a_y ?​

 

[zaper]

I'm really really sorry. I guess I'm way overthinking this or something. Is ax the radial acceleration?

 

[tiny-tim]

a is the acceleration

a_x and a_y are its x and y components

(i'm assuming you're using y for up and x for radial)

 

[zaper]

Ok so a_x is the radial acceleration and the total acceleration is pointing up and to the left. The triangle formed by the accelerations has top angle θ and a_y=a_x/tanθ. Is this correct? Also does a_y actually describe something here or is it just a component of the total a?

 

[tiny-tim]

… the total acceleration is pointing up and to the left.

what??

why? ​

 

[zaper]

Wait, I mean to the right

 

[tiny-tim]

Wait, I mean to the right

do you mean up and to the right, or only to the right?

 

[abhinav111]

hi zapper i have an easily understandable solution, if u have not come to the answer i may help.

 

[zaper]

Up and to the right tiny tim and what's your idea abhinav?

 

[tiny-tim]

Up and to the right

(along the normal?)

nooo

i think you're confusing physics and maths

force is physics

acceleration is maths (geometry)

if you know how the object is moving, then the acceleration follows automatically as a matter of maths

it doesn't matter what forces are producing that motion, the acceleration depends only on the motion, not on the forces

in this case, in equilibrium, the bead is moving uniformly in a horizontal circle …

so what is its acceleration? ​

 

[zaper]

Since there's no angular acceleration then the only acceleration is radial right?

 

[tiny-tim]

Since there's no angular acceleration then the only acceleration is radial right?

yes, but you're looking at the wrong radius …

the circle to look at is the circle of the bead's motion, which is horizontal, isn't it?

 

[zaper]

Yes. That last post was supposed to be in terms of the horizontal circle. Sorry that I forgot to explain that

 

[tiny-tim]

ok, so now do F_total = ma in both the horizontal and vertical directions

 

[zaper]

Ok I think we're getting back to my point of confusion from before. We've established that the only acceleration in the horizontal circle is the radial acceleration so I'm not quite seeing where this vertical force can come from unless you mean the weight

 

[tiny-tim]

yes, the weight is vertical

but the bead has no vertical acceleration …

so what's the other vertical force (that makes F=ma)? ​

 

[zaper]

The normal force? That's about all that's left

 

[tiny-tim]

The normal force? That's about all that's left

yes, N

N and mg are the only two forces on the bead

so their components in the vertical direction have to equal the component of ma in the vertical direction,

and their components in the horizontal direction have to equal the component of ma in the horizontal direction

 

[zaper]

Ok so N is the force pulling to the center of the hoop. Would it's x component have the force m*a_rad? Also the weight obviously has no x component so the only x force is from N.

 

[tiny-tim]

that's right!

so the x and y equations for F = ma are … ?​

 

[zaper]

Fy=N*cosθ-mg
Fx=m*a_rad=N*sinθ

Right?

 

[tiny-tim]

right!

so (without friction) ω = … ?​

 

[zaper]

Well a(rad)=Rw^2 so
w=(a/R)^1/2

(sorry I'm on my phone now and I can't do the fancy stuff so I'll be using "w" for omega)

 

[tiny-tim]

yes, but i mean what's the actual answer to the question …

what is ω as a function of θ ?​

(in other words: you have all the equations you need … now put them all together!)

 

[zaper]

what is ω as a function of θ ?

Not sure if this is what you want or not, but subbing Rω²=a_rad into Fx I get mRω²=N*sinθ.

Now if I solve this all out for θ will that be what I'm looking for?

 

[tiny-tim]

Not sure if this is what you want or not, but subbing Rω²=a_rad into Fx I get mRω²=N*sinθ.

but you're not told what N is!

(and that's not right anyway )

 

[zaper]

Ok so since we don't know what N is and the question doesn't ask for it we need to get rid of it. You said earlier that there is no vertical acceleration so that means N*cosθ=mg or N=mg/cosθ

 

[tiny-tim]

(just got up :zzz: …)

that's right …

now put everything together!​

 

[zaper]

So then plugging N into mrω2=N*sinθ (again r is the horizontal circle's radius) I get:

mrω²=mg*sinθ/cosθ

Simplified this is rω²=g*tanθ

Now I believe that r is R*sinθ so subbing again:

R*sinθ*ω²=g*tanθ which simplifies again to

R*ω²=g/cosθ

Hopefully I did all that right and from here it's easy to get θ by itself

 

[tiny-tim]

R*ω²=g/cosθ

yes!

ok, now you have ω as a function of θ, find both the normal force and the friction (tangential) force as a function of θ, and check whether µ is sufficient