JulienB
- 408
- 12
Homework Statement
Hi everybody! Here is a classical Bernoulli problem, which I'd like you to review to check if I (finally!) make a proper use of Bernoulli's equation!
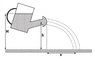
A gardener waters a bush with the help of a watering can (see attached pic). The water level in the can lays at height H = 1m, and the water flows horizontally out of the can at height h.
a) at which distance x from the bush must the water flow when the mouth of the can is located at h = 0.8m, in order for the water to reach the bush?
b) for which height h is x maximum? (we consider H is constant)
Homework Equations
Bernoulli equation, free fall and maybe a little bit of derivative?
The Attempt at a Solution
I think I get the point of the problem, but I often get confused
Hopefully this time I get it right:a) I first set up a Bernoulli equation between points (0) (behavior at height H) and (1) (mouth of the can at height h):
ρg(H - h) = ½⋅ρ⋅v12
(Here I considered P0 = P1 = 0 at gauge pressure, v0 = 0 and h the reference height)
⇔ v1 = √(2⋅g⋅(H - h)) = √(0.4⋅g)
Now from basic equations of motion I know:
horizontal displacement: x = v1⋅t
vertical displacement: -h = -½⋅g⋅t2
I solve for t using the second equation and get:
t = √(2h/g)
...and substitute it in the first one:
x = v1⋅t = √(0.8⋅h) = 0.8m
Is that correct?
b) Here I used the equation I found for velocity in a):
x = v⋅t = √(2g⋅(H - h))⋅√(2h/g) = 2√(hH - h2)
Here I wasn't sure what I should do so I simply took the derivative of (hH - h2) with respect to h and solved for which h it is equal to 0 (that is, when the function reaches a local critical point):
f'(h) = (hH - h2)' = H - 2h
f'(h) = 0 ⇔ h = ½⋅H = 0.5 m
Does that make sense? I get x = 1m, which is at least indeed bigger than in a). I'm sure there is also an easier method to get that result, but I couldn't figure it out yet. Any idea?Thank you very much in advance for your answers, I appreciate it.Julien.
