- #1
JulienB
- 408
- 12
Homework Statement
Hi everybody! I'm back with another Bernoulli problem :)
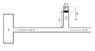
A reservoir with constant pressure P = 105 Pa releases through a tube water (density ρ = 1 g/cm3) with the velocity v = 4 m⋅s-1. That tube is then connected to another perpendicular tube (area A = 0.1 m2, height h = 2m) in which the water doesn't move and holds a mass m covering the whole area.
What is the mass m?
(sorry for the poor problem statement, it's hard to translate from German to English since neither of those languages are my mother language :) see attached picture for a better comprehension).
Homework Equations
Bernoulli equation, pressure, forces.
I also immediately convert ρ into ρ = 1000 Kg/m3.
The Attempt at a Solution
Okay I'm posting that problem here because I feel like I still get confused about how to deal with some inputs in the Bernoulli equation. Here is what I've done:
Since the mass is not moving, I believe ΣF = 0, which means that the force of the water on the mass (FU) is equal to the force of gravity of the mass on the water:
ΣF = 0 ⇔ mg = FU
Next step I want to know the pressure (P1) at the point where the water and the mass meet, and I am a little unsure about my formula:
P1 = FU/A = mg/a
Is that correct? I am often unsure what force should be placed in that equation...However I then attempted to substitute that pressure into my Bernoulli equation:
P + ρgh0 + ½ρv2 = P1 + ρgh + ½ρv12
(ρgh0 = 0 because h0 = 0, ½ρv12 = 0 since the water is not moving)
⇔ P + ½ρv2 = mg/A + ρgh
⇔ m = (A/g)(P + ½ρv2 - ρgh)
⇔ m = 880 Kg
What do you guys think?
Thank you very much in advance for your answers, I appreciate your help.Julien.