tomtomtom1
- 160
- 8
- TL;DR
- Bernoulli's Equation With Losses
Hello community
I have been trying to get my head around Bernoulli's equation when factoring in energy loss due to friction.
I am trying to understand the concepts and i was hoping someone could remove some doubt from my mind by confirming the following:-
1) Would the following statement be correct:-
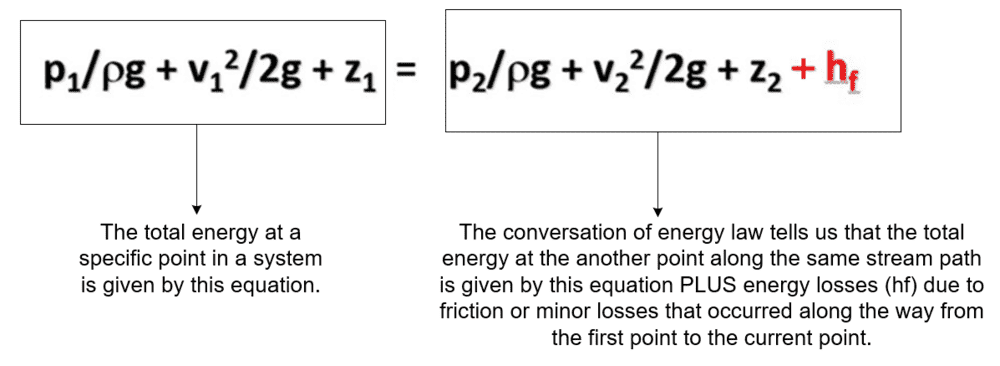
Is the above correct?
2) If i wanted to apply this equation to the following open channel system:-
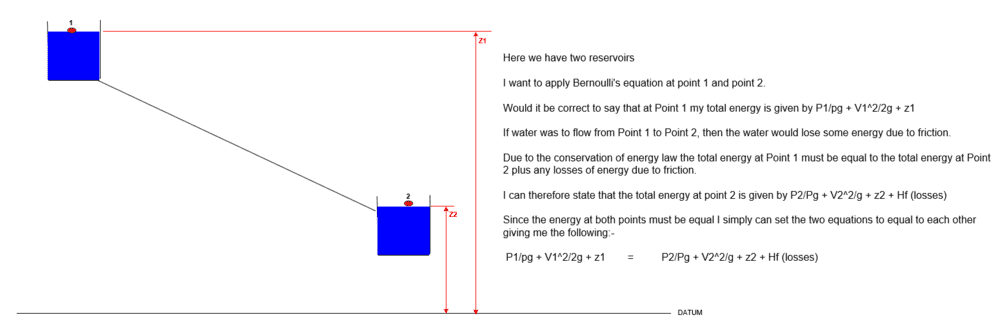 I am certain this is correct could really use someone with some experience to confirm this.
I am certain this is correct could really use someone with some experience to confirm this.
Thank you.
I have been trying to get my head around Bernoulli's equation when factoring in energy loss due to friction.
I am trying to understand the concepts and i was hoping someone could remove some doubt from my mind by confirming the following:-
1) Would the following statement be correct:-
Is the above correct?
2) If i wanted to apply this equation to the following open channel system:-
Thank you.