Billiard collision with same angle

[madman143]

Homework Statement

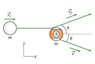
Jeanette is playing in a 9-ball pool tournament. She will win if she sinks the 9-ball from the final rack, so she needs to line up her shot precisely. Both the cue ball and the 9-ball have mass , and the cue ball is hit at an initial speed of . Jeanette carefully hits the cue ball into the 9-ball off center, so that when the balls collide, they move away from each other at the same angle from the direction in which the cue ball was originally traveling (see figure). Furthermore, after the collision, the cue ball moves away at speed , while the 9-ball moves at speed . (Intro 1 figure)

For the purposes of this problem, assume that the collision is perfectly elastic, neglect friction, and ignore the spinning of the balls.

pic attached

Homework Equations

v final=v

i get theta=cos^-1(v intial/2v)

please help. no numericals were given in this problem?

 

[LowlyPion]

First of all figures that Jeanette would choke on the money ball. But that said, don't you also need to conserve kinetic energy as well?

 

[LogicalTime]

you've got conservation of momentum along the x direction and along the y direction, see if you can throw those two equations down, then throw down one more with conservation of energy.