Alhussein
- 5
- 0
Biot-Savart's law of magnetic field " electromagnetic fields"
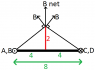
A rectangular loop carrying 10 A of current is placed on z=0 plane as shown in figure . Evaluate H at a) (2,2,0)
b) (4,2,0)
c) (4,8,0)
d) (0,0,2)
the used equation to answer the problem is
H= I/4∏ρ * (cosθ2-cosθ1) a∅
where ρ is the perpendicular distance between the line carrying current and the point which we need to evaluate H at
a∅=al X aρ
where aρ is a unit vector along the perpendicular line from the line current to the field point
i already answered a,b,c and I'm sure about the answers
but the number d is kinda hard . i solved it with many ways but it seems that I'm misunderstanding something here so i hoped that some1 can help me and tell me
what's the ρ and aρ is this situation . i just need to know how to get ρ and aρ in the future so i hope whoever answers will concentrate on showing me how to get it . thanks for helping me
http://www.mediafire.com/?21cwcskwt3yect4
Homework Statement
A rectangular loop carrying 10 A of current is placed on z=0 plane as shown in figure . Evaluate H at a) (2,2,0)
b) (4,2,0)
c) (4,8,0)
d) (0,0,2)
Homework Equations
the used equation to answer the problem is
H= I/4∏ρ * (cosθ2-cosθ1) a∅
where ρ is the perpendicular distance between the line carrying current and the point which we need to evaluate H at
a∅=al X aρ
where aρ is a unit vector along the perpendicular line from the line current to the field point
The Attempt at a Solution
i already answered a,b,c and I'm sure about the answers
but the number d is kinda hard . i solved it with many ways but it seems that I'm misunderstanding something here so i hoped that some1 can help me and tell me
what's the ρ and aρ is this situation . i just need to know how to get ρ and aρ in the future so i hope whoever answers will concentrate on showing me how to get it . thanks for helping me
http://www.mediafire.com/?21cwcskwt3yect4
Last edited by a moderator: