Max Loo Pin Mok
- 5
- 7
The following are 3 equations of Planck's law or Planck's distribution function. Are they all correct? How do they derive from each other?
Equation One:
From page 512 of http://metronu.ulb.ac.be/npauly/art_2014_2015/shockley_1961.pdf
We denote by Qs the number of quanta of frequency greater than vg incident per unit area per unit time for black-body radiation of temperature Ts. For later purposes we shall also introduce the symbol Qs(vg, Ts) in order to be able to represent situations for different values of the limiting frequency.
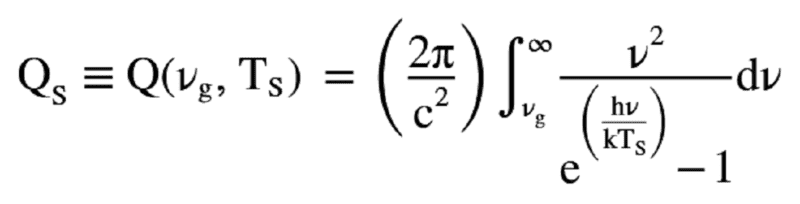
Equation Two:
From page 1 of https://edisciplinas.usp.br/pluginfile.php/48089/course/section/16461/qsp_chapter10-plank.pdf
Energy density of radiation per unit frequency interval u(v) for black-body radiation is described by the Planck formula:
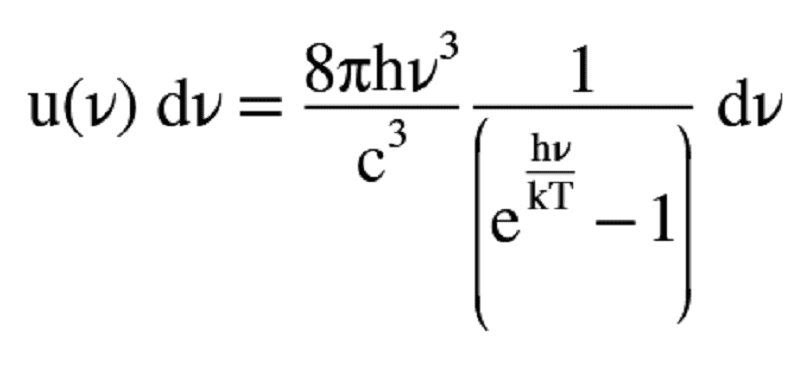
Equation Three:
From https://en.wikipedia.org/wiki/Planck's_law
The spectral radiance of a body, Bv, describes the amount of energy it gives off as radiation of different frequencies. It is measured in terms of the power emitted per unit area of the body, per unit solid angle that the radiation is measured over, per unit frequency. The SI unit of spectral radiance in frequency is the watt per steradian per square metre per hertz (W·sr-1·m-2·Hz-1).
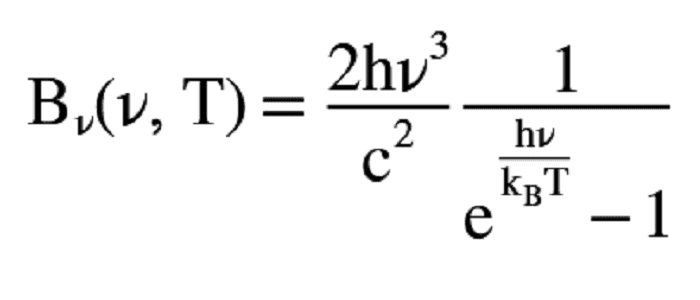
Equation One:
From page 512 of http://metronu.ulb.ac.be/npauly/art_2014_2015/shockley_1961.pdf
We denote by Qs the number of quanta of frequency greater than vg incident per unit area per unit time for black-body radiation of temperature Ts. For later purposes we shall also introduce the symbol Qs(vg, Ts) in order to be able to represent situations for different values of the limiting frequency.
Equation Two:
From page 1 of https://edisciplinas.usp.br/pluginfile.php/48089/course/section/16461/qsp_chapter10-plank.pdf
Energy density of radiation per unit frequency interval u(v) for black-body radiation is described by the Planck formula:
Equation Three:
From https://en.wikipedia.org/wiki/Planck's_law
The spectral radiance of a body, Bv, describes the amount of energy it gives off as radiation of different frequencies. It is measured in terms of the power emitted per unit area of the body, per unit solid angle that the radiation is measured over, per unit frequency. The SI unit of spectral radiance in frequency is the watt per steradian per square metre per hertz (W·sr-1·m-2·Hz-1).