Block moving on an inclined plane

[utkarshakash]

Homework Statement

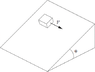
A block is placed on a plane inclined at an angle θ. The coefficient of friction between the block and the plane is µ = tan θ. The block is given a kick so that it initially moves with speed V horizontally along the plane (that is, in the direction perpendicular to the direction pointing straight down the plane). What is the speed of the block after a very long time?

The Attempt at a Solution

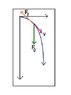
The force of friction exactly balances the gravitational force along the incline. So there will be no acceleration along the inclined plane and the trajectory of the block must be a straight line and it continues to move in its original direction of motion. The frictional force will act opposite to its velocity and after a long time the block should stop. So the final velocity should be 0. But this is not the correct answer. I can't figure out what's wrong with my reasoning.

 

[voko]

You are ignoring the fact that the force of kinetic friction is always aligned with the velocity. So initially it is purely horizontal and does not oppose the force of gravity that pulls the block sideways, so the velocity vector gets a sideways component, so does the force of friction, etc.

 

[utkarshakash]

You are ignoring the fact that the force of kinetic friction is always aligned with the velocity. So initially it is purely horizontal and does not oppose the force of gravity that pulls the block sideways, so the velocity vector gets a sideways component, so does the force of friction, etc.

So how should I proceed?

 

[voko]

The first step here would be to write down the components of the net force acting on the particle in the plane of the incline.

 

[utkarshakash]

The first step here would be to write down the components of the net force acting on the particle in the plane of the incline.

The net force is mgsinα down the incline and frictional force = mgsinα opposite the direction of initial velocity

 

[voko]

It would be useful to have that written as differential equations.

 

[ehild]

The net force is mgsinα down the incline and frictional force = mgsinα opposite the direction of [STRIKE]initial [/STRIKE]velocity

The force of friction is opposite to the instantaneous velocity.

ehild

 

[haruspex]

Unless I missed some smart method, this is quite a tough problem.
I managed to solve it using Whewell (s, psi) coordinates. See http://en.wikipedia.org/wiki/Whewell_equation.

 

[voko]

There is a very simple integral that can be reached via a mathematical device, or physical intuition.

 

[ehild]

Unless I missed some smart method, this is quite a tough problem.
I managed to solve it using Whewell (s, psi) coordinates. See http://en.wikipedia.org/wiki/Whewell_equation.

You do not need to solve the differential equation. The problem asks the speed after very long time.
If you write the differential equations for the velocity components along the slope(v_x) and in the horizontal direction (v_y), and also the derivative of the speed v, you get a very simple relation between dv/dt and dv_x/dt. Also, it is easy to figure out the long-term behaviour of v_y.

But I would like to see the solution for v(t)...

ehild

 

[dauto]

You do not need to solve the differential equation. The problem asks the speed after very long time.
If you write the differential equations for the velocity components along the slope(v_x) and in the horizontal direction (v_y), and also the derivative of the speed v, you get a very simple relation between dv/dt and dv_x/dt. Also, it is easy to figure out the long-term behaviour of v_y.

But I would like to see the solution for v(t)...

ehild

Agreed. I would like to see the complete solution as well.

 

[haruspex]

You do not need to solve the differential equation. The problem asks the speed after very long time.
If you write the differential equations for the velocity components along the slope(v_x) and in the horizontal direction (v_y), and also the derivative of the speed v, you get a very simple relation between dv/dt and dv_x/dt. Also, it is easy to figure out the long-term behaviour of v_y.

But I would like to see the solution for v(t)...

ehild

Ok.
The forces are mg sin(θ) down the plane, and likewise in the direction opposite to the velocity.
In (s, ψ) coordinates, with ψ as the angle of the velocity to the horizontal in the plane,
$\ddot s = (\sin(\psi)-1)g \sin(\theta)$
$\dot s \dot \psi = g \sin(\theta) \cos(\psi)$
Writing $\dot s = g \sin(\theta) u$, this simplifies to
$\dot u = (\sin(\psi)-1)$
$u \dot \psi = \cos(\psi)$
Eliminating u we get:
$\dot\psi^2(1-2 \sin(\psi)) = \ddot \psi \cos(\psi)$, with initial conditions $\psi(0) = 0, \dot \psi(0) = \frac 1{u(0)} = \frac v{g \sin(\theta)}$
Rewriting that as $\dot\psi(\sec(\psi)-2 \tan(\psi)) = \frac{\ddot \psi }{\dot \psi }$ we can integrate to obtain
$\dot \psi = A \cos(\psi)(1+\sin(\psi))$, $u = \frac 1{A(1+\sin(\psi))}$
The initial conditions give $A = \frac{g \sin(\theta)}{v}$, so $\dot s = \frac v {(1+\sin(\psi))}$
We want $\mathop{\lim}_{t\rightarrow \infty}\dot s = \mathop{\lim}_{\psi\rightarrow \frac{\pi}{2}}\dot s = \frac v2$
(What's a better way to write limits in LaTex?)
You could also solve to find t as a function of ψ.

 

[ehild]

We want $\mathop{\lim}_{t\rightarrow \infty}\dot s = \mathop{\lim}_{\psi\rightarrow \frac{\pi}{2}}\dot s = \frac v2$
(What's a better way to write limits in LaTex?)
You could also solve to find t as a function of ψ.

$$\mathop{\lim}_{t\rightarrow \infty}\dot s = \mathop{\lim}_{\psi\rightarrow \frac{\pi}{2}}\dot s = \frac v2$$

Use $$ instead of ##, but then it becomes a new line.

ehild

 

[voko]

Nicely done, haruspex. For limits, there is a "limits" modifier that forces indices above and below the current symbol: $\lim\limits^{up}_{down} \int\limits_{from}^{to}\sum\limits_{begin}^{end}$.

 

[utkarshakash]

Ok.
The forces are mg sin(θ) down the plane, and likewise in the direction opposite to the velocity.
In (s, ψ) coordinates, with ψ as the angle of the velocity to the horizontal in the plane,
$\ddot s = (\sin(\psi)-1)g \sin(\theta)$
$\dot s \dot \psi = g \sin(\theta) \cos(\psi)$
Writing $\dot s = g \sin(\theta) u$, this simplifies to
$\dot u = (\sin(\psi)-1)$
$u \dot \psi = \cos(\psi)$
Eliminating u we get:
$\dot\psi^2(1-2 \sin(\psi)) = \ddot \psi \cos(\psi)$, with initial conditions $\psi(0) = 0, \dot \psi(0) = \frac 1{u(0)} = \frac v{g \sin(\theta)}$
Rewriting that as $\dot\psi(\sec(\psi)-2 \tan(\psi)) = \frac{\ddot \psi }{\dot \psi }$ we can integrate to obtain
$\dot \psi = A \cos(\psi)(1+\sin(\psi))$, $u = \frac 1{A(1+\sin(\psi))}$
The initial conditions give $A = \frac{g \sin(\theta)}{v}$, so $\dot s = \frac v {(1+\sin(\psi))}$
We want $\mathop{\lim}_{t\rightarrow \infty}\dot s = \mathop{\lim}_{\psi\rightarrow \frac{\pi}{2}}\dot s = \frac v2$
(What's a better way to write limits in LaTex?)
You could also solve to find t as a function of ψ.

Can you please explain what have you done here? It's difficult for me to follow your approach. What does (s,ψ) coordinates mean here?

 

[voko]

Can you please explain what have you done here? It's difficult for me to follow your approach. What does (s,ψ) coordinates mean here?

You do not need to follow that. Use the approach mentioned by ehild.

 

[TSny]

utkarshakash,

Remember the thread https://www.physicsforums.com/showthread.php?t=748236.

Can you see that this is virtually the same problem?

 

[utkarshakash]

utkarshakash,

Remember the thread https://www.physicsforums.com/showthread.php?t=748236.

Can you see that this is virtually the same problem?

Yes. I still remember this thread and I see this problem is exactly the same. Thanks!

 

[haruspex]

Can you please explain what have you done here? It's difficult for me to follow your approach. What does (s,ψ) coordinates mean here?

As ehild and voko point out, there's a much easier way to obtain $\dot s = \frac{v}{1+\sin(\psi)}$. If not, I would have given hints, not posted my calculus solution in detail.
In (s,ψ) coordinates, s is the distance along the path from some fixed origin, and ψ is the angle the path makes to some fixed direction at that point. (I chose that to be the initial direction of motion, with positive ψ being down the plane.) The link I posted shows how to convert to and from other systems.
It gives much simpler differential equations in some cases, like this one. The acceleration along the path, $\ddot s$, comes from the frictional force plus the sin(ψ) component of the downplane gravitational force:
$\ddot s = (\sin(\psi)-1)g \sin(\theta)$
The acceleration normal to the path, $\dot s \dot \psi$, comes from the cos(ψ) component of the downplane gravitational force:
$\dot s \dot \psi = g \sin(\theta) \cos(\psi)$
Since g sin(θ) occurs as a common factor, it can be eliminated by incorporating it into s.

 

[ehild]

Cartesian coordinates might be used, too, and that approach might be more familiar to the OP.

The x-axis is horizontal, directed along the initial velocity. The y-axis is parallel with the slope, pointing downward. See picture.

The downward force is Fg=mgsinθ. The magnitude of the force of friction is also mgsinθ. The force of friction is opposite to the velocity v. It can be written as the negative of the magnitude multiplied by the unit vector in the direction of the velocity $$\vec F_f=-mgsinθ \frac{\vec v}{v}$$
If v_x, v_y are the components of the velocity and v is the speed $v= \sqrt{v_x^2+v_y^2}$ the horizontal component of the friction is $-mg\sinθ \frac{v_x}{v}$ and the vertical component is $-mg\sinθ \frac{v_y}{v}$.

Write out the x and y components of acceleration, and also the time derivative of the speed v. Use the notation A=gsinθ.

$$\dot v_x=-A\frac{v_x}{v}$$
$$\dot v_y=A(1-\frac{v_y}{v})$$

$$\dot v=\frac{v_x \dot v_x +v_y \dot v_y}{v}$$

Substitute the first two equations for v_x, v_y into the third one. You will see that the time derivative of v_y is equal and opposite to that of v. Integrate.

It can be proved mathematically, but it is clear that the horizontal component of the velocity tends to zero with time, so the speed becomes equal to the vertical velocity component v→v_y.

ehild

 

[haruspex]

Cartesian coordinates might be used, too, and that approach might be more familiar to the OP.

The x-axis is horizontal, directed along the initial velocity. The y-axis is parallel with the slope, pointing downward. See picture.

The downward force is Fg=mgsinθ. The magnitude of the force of friction is also mgsinθ. The force of friction is opposite to the velocity v. It can be written as the negative of the magnitude multiplied by the unit vector in the direction of the velocity $$\vec F_f=-mgsinθ \frac{\vec v}{v}$$
If v_x, v_y are the components of the velocity and v is the speed $v= \sqrt{v_x^2+v_y^2}$ the horizontal component of the friction is $-mg\sinθ \frac{v_x}{v}$ and the vertical component is $-mg\sinθ \frac{v_y}{v}$.

Write out the x and y components of acceleration, and also the time derivative of the speed v. Use the notation A=gsinθ.

$$\dot v_x=-A\frac{v_x}{v}$$
$$\dot v_y=A(1-\frac{v_y}{v})$$

$$\dot v=\frac{v_x \dot v_x +v_y \dot v_y}{v}$$

Substitute the first two equations for v_x, v_y into the third one. You will see that the time derivative of v_y is equal and opposite to that of v. Integrate.

It can be proved mathematically, but it is clear that the horizontal component of the velocity tends to zero with time, so the speed becomes equal to the vertical velocity component v→v_y.

ehild

I had thought your argument was even simpler. The frictional and downslope gravitational forces are equal, so, by symmetry, the acceleration along the path (but measured in the backward direction) and the downslope acceleration must be equal. So the corresponding two speeds have a constant difference, namely, the initial speed. In the limit, the two speeds are equal and opposite, so must each be v/2 in magnitude.

 

[voko]

The frictional and downslope gravitational forces are equal, so, by symmetry, the acceleration along the path (but measured in the backward direction) and the downslope acceleration must be equal.

That was the physical intuition I mentioned. It was difficult to allude to in a hint without telling the full story.

 

[ehild]

I had thought your argument was even simpler. The frictional and downslope gravitational forces are equal, so, by symmetry, the acceleration along the path (but measured in the backward direction) and the downslope acceleration must be equal. So the corresponding two speeds have a constant difference, namely, the initial speed. In the limit, the two speeds are equal and opposite, so must each be v/2 in magnitude.

Your argument is very clever, but it is difficult to formulate exactly. For example, speed is magnitude, never negative. It can not be said that the two speeds are equal and opposite. In my derivation, the downward velocity is positive and the speed v is also positive (as it is speed) and the accelerations are equal and opposite, so the sum of vy and v is constant. (v_y+v=V)

I am a bit slow in thinking, so prefer writing some equations .

ehild