Blocks, incline, tension and acceleration

[noob314]

Homework Statement

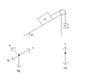
A large block of mass M = 6kg is on an incline which is at an angle of 30 degrees above the horizontal. The coefficient of kinetic friction between the block and the incline is 0.3. The block is attached to a string which runs over a pulley and is connected to a smaller block of mass m = 2.4 kg.

If the block is sliding up the incline, find a) the acceleration (magnitude and direction) of the smaller block m and b) the tension in the string.

The Attempt at a Solution

I need someone to confirm if what I'm doing is correct.

a)
\Sigma \vec{F}_{M} = Ma = T - f_{k} - Mgsin\theta
T = M(gsin\theta + a + \mu_{k}gcos\theta)
\Sigma\vec{F}_{m} = ma = mg - T
= mg - M(gsin\theta + a + \mu_{k}gcos\theta)
= ma + Ma = mg - Mgsin\theta - \mu_{k}Mgcos\theta
= a(m+M) = mg - Mgsin\theta - \mu_{k}Mgcos\theta
= a = \frac{mg - Mgsin\theta - \mu_{k}Mgcos\theta}{m+M}
= a = -2.52\frac{m}{s^{2}}
I'm guessing this is the acceleration in the y-direction, and the acceleration in the x-direction would be 0, so the magnitude is 2.52
= 2.52\frac{m}{s^{2}} down

b)
\Sigma\vec{F}_{m} = mg - T = ma
T = mg - ma
= (2.4kg)(9.80 \frac{m}{s^{2}}) - (2.4kg)(2.52\frac{m}{s^{2}})
= 17.47N

Which looks about right, since in order for m to be moving down, mg needs to be greater than T, which in this case it is.

 

[PhanthomJay]

I haven't checked your equations, but you should first check the wording of the problem. The block can't be sliding up the plane, the hanging mass is too small to haul it up. It can't be sliding down the plane, either. Did you copy the problem down correctly?

 

[noob314]

Yes, the problem is copied down correctly.

 

[PhanthomJay]

Yes, the problem is copied down correctly.

Then someone made a boo-boo. The problem makes no sense as written.

 

[noob314]

Is it really impossible? I assumed some unknown force allowed it to overcome whatever static friction there may have been which would have allowed mass m to overcome the kinetic friction.

 

[PhanthomJay]

Is it really impossible? I assumed some unknown force allowed it to overcome whatever static friction there may have been which would have allowed mass m to overcome the kinetic friction.

What unknown force?

 

[noob314]

I assume it would be a force that's barely able to overcome the static friction and then disappear after that.

 

[PhanthomJay]

The more you try to make sense of this problem, the more it will confuse you. Just rip it up and try another problem.

 

[noob314]

Yeah, you're right. I rechecked my calculations and the numbers didn't add up. I was just curious because it was on one of my old exams.