FocusedWolf
- 81
- 0
Hi,
This is a question about a boolean "law" type behavior I've noticed in my homework a couple of times.
Basically i can't find a boolean algebra law that permits this optimization short of using a k-map.
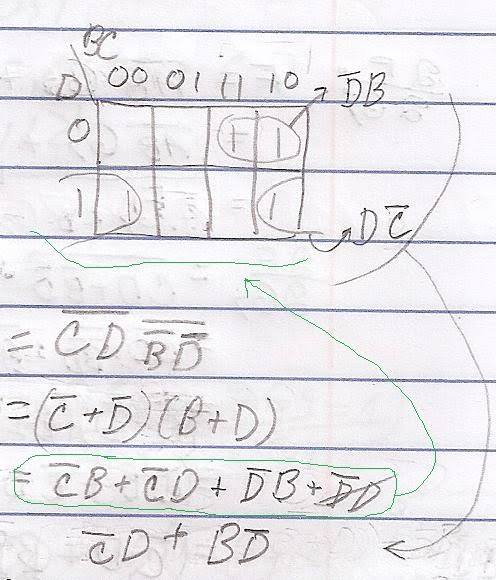
So I'm just wondering if theirs some way to optimize the one equation using just boolean algebra in order to get the second one (the output of the k-map).
This is a question about a boolean "law" type behavior I've noticed in my homework a couple of times.
Basically i can't find a boolean algebra law that permits this optimization short of using a k-map.
So I'm just wondering if theirs some way to optimize the one equation using just boolean algebra in order to get the second one (the output of the k-map).