Boundary Conditions for an infinite rectangular pipe

AI Thread Summary
The discussion centers on the appropriate boundary conditions and axis assignments for modeling an infinite rectangular pipe. Participants clarify their axis definitions, agreeing that the pipe is infinite along the X-axis, with the Y-axis representing width and Z-axis being vertical. There is consensus that the problem can be treated as a 2-D Laplace equation, as the infinite length along the Z-axis makes it independent of that dimension. The voltage conditions are specified, with V on the Y-axis faces and 0 on the Z-axis faces. Overall, the focus is on ensuring correct boundary conditions and axis orientation before proceeding with the solution.
guyvsdcsniper
Messages
264
Reaction score
37
Homework Statement
An infinite rectangular pipe with sides a, has two opposite sides at voltage V
(front and back) and at voltage V=0 (top and bottom).

Find the potential inside the pipe.
Relevant Equations
Fourier Sine Trick
Does setting up the problem symmetrically on this axis and the boundary conditions applied make sense? I don't believe I will have a problem solving for the potential inside, but i just want to make sure I have my B.C and axis correct before proceeding.

IMG_0381.jpg


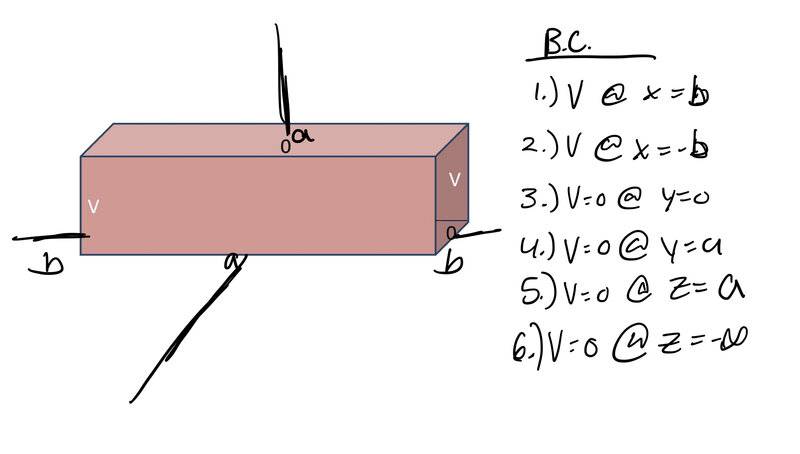
EDIT:

Or should this be a 2-D lapace equation since the pipe is infinitely long, making this independent of the z axis?
 
Last edited:
Physics news on Phys.org
I'm a bit confused about how you are assigning the axes.
I'll call the left right axis X, the vertical axis Z and the lower left/ upper right axis in the picture Y. From that and the text description, I would say the pipe is infinite in the X axis and width a in the other two. The voltage is V on the faces normal to the Y axis and 0 on those normal to the Z axis.
 
haruspex said:
I'm a bit confused about how you are assigning the axes.
I'll call the left right axis X, the vertical axis Z and the lower left/ upper right axis in the picture Y. From that and the text description, I would say the pipe is infinite in the X axis and width a in the other two. The voltage is V on the faces normal to the Y axis and 0 on those normal to the Z axis.
Sorry I missed that. y is the vertical axis.z is the axis coming out of the page. X is horizontal.

But I think it should be independent of Z since it is infinitely long. It mirrors an example straight out my textbook.
 
quittingthecult said:
z is the axis coming out of the page.
quittingthecult said:
independent of Z since it is infinitely long.
Looking at the diagram, the infinitely long direction is horizontal.
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »
Thread 'Minimum mass of a block'

Thread 'Minimum mass of a block'

Here we know that if block B is going to move up or just be at the verge of moving up ##Mg \sin \theta ## will act downwards and maximum static friction will act downwards ## \mu Mg \cos \theta ## Now what im confused by is how will we know " how quickly" block B reaches its maximum static friction value without any numbers, the suggested solution says that when block A is at its maximum extension, then block B will start to move up but with a certain set of values couldn't block A reach...
View full post »

Similar threads

Potential inside a rectangular pipe
Replies
2
Views
1K
Evaluating the boundary conditions for a rectangular pipe
Replies
19
Views
2K
Find potential within a pipe using Laplace's equation
Replies
18
Views
2K
Understanding a math step in solving Schrödinger's equation for single particle in a box
Replies
8
Views
905
Boundary conditions in dielectric problems
Replies
2
Views
3K
Potential in the three regions of an infinite slab
Replies
1
Views
1K
Correct Setup for Finite Difference to Calculate Quantum Tunneling
Replies
2
Views
917
How electric potential boundary condition works
Replies
5
Views
3K
Laplacian for hyperbolic plates
Replies
26
Views
2K
A Why is "method of image current" valid in magnetostatics?
Replies
4
Views
2K

Hot Threads

Recent Insights

Back
Top