jaus tail
- 613
- 48
Hi,
I'm studying Choppers and I'm struggling with derivation of Buck Converter.
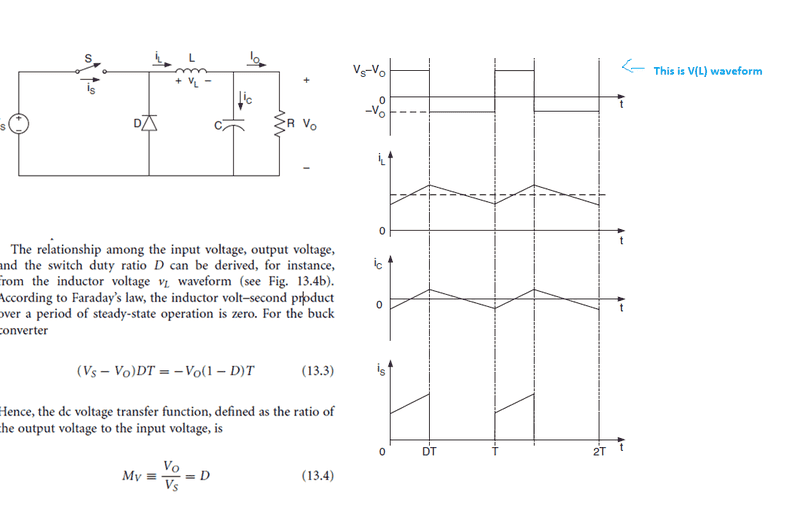
As per equation 13.3 if I solve it ahead I get
Vs D T - Vo D T = - Vo T + Vo D T
Solving this ahead I get
Vs (D T ) = Vo (-T + DT + DT)
Vs (DT) = Vo(2DT - T)
Vs D = Vo (2D - 1)
Vo / Vs = D/(2D - 1)
Not sure how to go ahead from here to reach equation 13.4
I'm studying Choppers and I'm struggling with derivation of Buck Converter.
As per equation 13.3 if I solve it ahead I get
Vs D T - Vo D T = - Vo T + Vo D T
Solving this ahead I get
Vs (D T ) = Vo (-T + DT + DT)
Vs (DT) = Vo(2DT - T)
Vs D = Vo (2D - 1)
Vo / Vs = D/(2D - 1)
Not sure how to go ahead from here to reach equation 13.4


