Much better. I think your work is correct. I solved the integral differently, using to applications of integration by parts. As I said before, you really need to simplify your answer. I think you have a correct expression, but you need to combine your terms and put them over a common denominator.
The earlier parts of the problem are supposed to help later on! They can really save you a lot of work. For instance, I knew by inspection that all the a_n were 0 just by observing that f is an odd function. Similarly, you can simplify the calculation of the b_n by noting that the integrand is even.
So try simplifying your answer. Look for cancellation in terms of the form (-1)^k + 1, too. I think this will make the choice for x a lot easier.
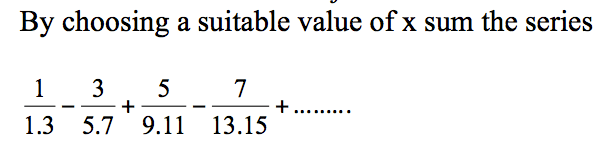 Here's my thought so far:
Here's my thought so far: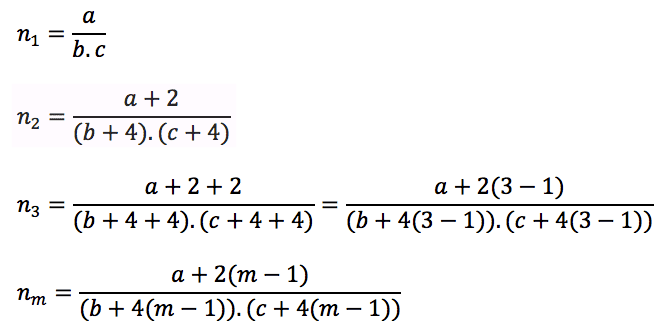 This is pretty much what I have come up with. However, I don't know how to find a general solution for the sum of the series. Can someone help please. (the decimal part is where I'm stuck the most)
This is pretty much what I have come up with. However, I don't know how to find a general solution for the sum of the series. Can someone help please. (the decimal part is where I'm stuck the most)


