Calculate Area of Tree Structure (Wondering)

[mathmari]

Hey!

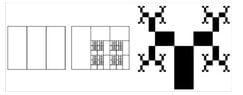
A DIN A4 sheet is divided into thirds. A rectangle is the root of the tree, the other two rectangles are each divided into thirds again. Two rectangles form the branches - one to the left, one to the right - the others are again divided into thirds and so on.

View attachment 8105

I want to calculate the area of that tree. I understood teh mathod as follows:
First we have the whole sheet.
Then we divide it into three parts.
Then all except of $2^0=1$ part are again divided into three parts.
Then all except of $2^1=2$ parts again again divided into three parts.
Then all except of $2^2=4$ parts again again divided into three parts.
and so on I mean something like that:

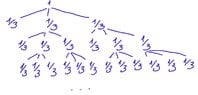
View attachment 8106 So at level i of the tree we divide all parts except of $2^i$ into three parts. Have I undersood that correctly? (Wondering)

How can we calculate the area? Do we maybe have to write the above as a recursive function? (Wondering)

 

[castor28]

Hi mathmari,

Note that all those trees are similar. Specifically, each of the two subtrees on top of the initial rectangle has an area equal to $\dfrac13$ of the whole tree.

If $T$ is the area of the whole tree and $S$ the area of the initial rectangle, we have:
$$T = S + \frac23 T$$
which shows that $T=3S$; this is the area of the whole A4 sheet, i.e., $\dfrac{1}{16}\,\mathrm{m}^2$.

 

[mathmari]

Note that all those trees are similar. Specifically, each of the two subtrees on top of the initial rectangle has an area equal to $\dfrac13$ of the whole tree.

If $T$ is the area of the whole tree and $S$ the area of the initial rectangle, we have:
$$T = S + \frac23 T$$
which shows that $T=3S$; this is the area of the whole A4 sheet, i.e., $\dfrac{1}{16}\,\mathrm{m}^2$.

So, each tree consists of a rectagle and two subtrees, and so the area of the big tree is equal to the area of the rectangle + the area of the subtrees.
Have I understood it correctly so far?

Why has each of the two subtrees on top of the initial rectangle an area equal to $\dfrac13$ of the whole tree? Because we use the $\frac{1}{3}$ to create that? We have that $S$ is equal to $\frac{1}{3}$ of the area of the A4 sheet, isn't it? Which is this area? (Wondering)

 

[castor28]

So, each tree consists of a rectagle and two subtrees, and so the area of the big tree is equal to the area of the rectangle + the area of the subtrees.
Have I understood it correctly so far?

Why has each of the two subtrees on top of the initial rectangle an area equal to $\dfrac13$ of the whole tree? Because we use the $\frac{1}{3}$ to create that? We have that $S$ is equal to $\frac{1}{3}$ of the area of the A4 sheet, isn't it? Which is this area? (Wondering)

Hi mathmari,

That is correct so far.

Now that I think a bit more about it, I realize that what I wrote is not correct (although the final result is correct by chance;)); sorry for that .

The horizontal rectangles are not similar to the vertical rectangles, contrary to what I first thought. What is true is that all the horizontal rectangles are similar to each other, and all the vertical rectangles are similar to each other.

To see this, note that to get the next smaller vertical rectangle, you divide both the width and the height of the current vertical rectangle by 3. This also shows that the area of a vertical rectangle is $\dfrac19$ the area of the next larger vertical rectangle, and the same holds for horizontal rectangles. This shows that all the vertical subtrees are similar to each other (and the same holds for horizontal subtrees).

Now, the whole tree (of unknown area $T$) consists of:

• One vertical rectangle of area $S$ (the "trunk"). This is $\dfrac13$ of an A4 sheet.
• Two horizontal rectangles of area $\dfrac{S}{3}$ each.
• Four subtrees similar to the whole tree. As the ratio of the vertical rectangles (the "trunks") is $\dfrac19$, each of these 4 subtrees has an area of $\dfrac{T}{9}$

This leads to the equation:
$$ T = S + \frac23S + \frac49T$$
which still gives $T=3S$.

As $S$ is one third of an A4 sheet, $T$ is one full A4 sheet. By definition, one DIN A0 sheet has an area of one square meter and a side ratio of $\sqrt2$. An A(n+1) sheet is one half on an A(n) sheet; this gives an area of $\dfrac{1}{16}\,\mathrm{m}^2$ for an A4 sheet.

 

[mathmari]

The horizontal rectangles are not similar to the vertical rectangles, contrary to what I first thought. What is true is that all the horizontal rectangles are similar to each other, and all the vertical rectangles are similar to each other.

To see this, note that to get the next smaller vertical rectangle, you divide both the width and the height of the current vertical rectangle by 3. This also shows that the area of a vertical rectangle is $\dfrac19$ the area of the next larger vertical rectangle, and the same holds for horizontal rectangles. This shows that all the vertical subtrees are similar to each other (and the same holds for horizontal subtrees).

Now, the whole tree (of unknown area $T$) consists of:

• One vertical rectangle of area $S$ (the "trunk"). This is $\dfrac13$ of an A4 sheet.
• Two horizontal rectangles of area $\dfrac{S}{3}$ each.
• Four subtrees similar to the whole tree. As the ratio of the vertical rectangles (the "trunks") is $\dfrac19$, each of these 4 subtrees has an area of $\dfrac{T}{9}$

I haven't really understood that. Could you explain this further to me? (Wondering)

 

[I like Serena]

Hey mathmari! (Wave)

I'm a bit confused.
If we follow the algorithm in the first 2 pictures, we won't get the tree in the 3rd picture will we?
Can you clarify? (Wondering)

Btw, this looks like a fractal structure that seems to have surface area 0. Fractals typically have a 'broken' dimension. (Thinking)

 

[mathmari]

I'm a bit confused.
If we follow the algorithm in the first 2 pictures, we won't get the tree in the 3rd picture will we?
Can you clarify? (Wondering)

Why not? The one of the three parts that is not divided into three, is placed on the tree? Or not? (Wondering)

Btw, this looks like a fractal structure that seems to have surface area 0. Fractals typically have a 'broken' dimension. (Thinking)

What does this mean? (Wondering)

 

[I like Serena]

Why not? The one of the three parts that is not divided into three, is placed on the tree? Or not?

It doesn't look like that... (Thinking)

Hmm... if I understand correctly, and looking at the final tree, it works like this.
Let w=297mm and h=210mm.
Then the trunk seems to have width w/9 and height h/3, doesn't it?
And then we have 2 branches that each have width w/9 and height h/9, yes?
Those fork into 4 branches that each have width w/27 and height h/9.
Is that how it works? (Wondering)

What does this mean? (Wondering)

It seems that in this particular case we can get a non-zero area after all, so you can ignore my comment.

Either way, I was referring to the famous Koch curve that has infinite length and the curve itself has an area of 0 square units.
To find a meaningful length we need to measure it in $\text{unit}^{\ln 4 /\ln 3}\approx \text{unit}^{1.26}$.
That is, the so called Hausdorf dimension of the Koch curve is $D=1.26$.

 

[I like Serena]

Is it like this? (Wondering)
View attachment 8109

Units are in millimeters and a DIN A4 is 297 mm x 210 mm.

 

[mathmari]

Yes! Looking at that picture, do we have the following?

Let $S_n$ be the area of the rectangular at the $n$-th step.

From each rectangullar of area $S_n$ we get two new rectangulars with total area $\frac{2}{3}\cdot S_n$, i.e. each has area $\frac{1}{3}\cdot S_n$.

This holds because each rectangular gets into three pieces, and two of the three pieces are the branches of the rectanglar.

Let $S_0$ be the area of the DIN A4 sheet. Then $S_1=\frac{1}{3}\cdot S_0$, is the area of the one of the three pieces, which is the root of the tree.

The area of the tree is then equal to
$$S_1+\frac{2}{3}\cdot S_1+\left (\frac{2}{3}\right )^2\cdot S_1+\left (\frac{2}{3}\right )^3\cdot S_1+\ldots=\sum_{i=0}^{\infty}\left (\frac{2}{3}\right )^i\cdot S_1$$Is this correct? Or haven't understood correctly the idea? (Wondering)

 

[I like Serena]

Yes! Looking at that picture, do we have the following?

Let $S_n$ be the area of the rectangular at the $n$-th step.

From each rectangullar of area $S_n$ we get two new rectangulars with total area $\frac{2}{3}\cdot S_n$, i.e. each has area $\frac{1}{3}\cdot S_n$.

This holds because each rectangular gets into three pieces, and two of the three pieces are the branches of the rectanglar.

Let $S_0$ be the area of the DIN A4 sheet. Then $S_1=\frac{1}{3}\cdot S_0$, is the area of the one of the three pieces, which is the root of the tree.

The area of the tree is then equal to
$$S_1+\frac{2}{3}\cdot S_1+\left (\frac{2}{3}\right )^2\cdot S_1+\left (\frac{2}{3}\right )^3\cdot S_1+\ldots=\sum_{i=0}^{\infty}\left (\frac{2}{3}\right )^i\cdot S_1$$Is this correct? Or haven't understood correctly the idea? (Wondering)

All correct. (Nod)

It's just that if the whole tree is supposed to fit on an A4, that the trunk must be a rectangle with area $\frac 19\cdot \frac 13 \cdot S_0=\frac 1{27}S_0$.
That is what I have drawn and what seemed to match with picture 2 in the OP.
Or is the tree supposed to grow bigger than an A4? (Wondering)

 

[mathmari]

All correct. (Nod)

Could I improve something at the justifications, or they ok in that way? (Wondering)

It's just that if the whole tree is supposed to fit on an A4, that the trunk must be a rectangle with area $\frac 19\cdot \frac 13 \cdot S_0=\frac 1{27}S_0$.
That is what I have drawn.
Or is the tree supposed to grow bigger than an A4? (Wondering)

I don't really know. It doesn't say anything in the exercise statement about that.

So, if it can be bigger then we have that $S_1=\frac{1}{3}\cdot S_0$ and if not then $S_1=\frac{1}{27}\cdot S_0$ ?

How do we get that $\frac{1}{9}$ ?

(Wondering)

 

[I like Serena]

Could I improve something at the justifications, or they ok in that way?

I believe your justifications are just fine, and I wouldn't know what to improve. (Happy)

I don't really know. It doesn't say anything in the exercise statement about that.

So, if it can be bigger then we have that $S_1=\frac{1}{3}\cdot S_0$ and if not then $S_1=\frac{1}{27}\cdot S_0$ ?

How do we get that $\frac{1}{9}$ ?

I was looking at picture 2 and tried to find the trunk in there.
The best I could find is the rectangle at the bottom with 1/9th of the width and 1/3rd of the height... (Thinking)

Hmm... rereading the OP, it seems intended that after the initial division into 3 rectangles, one of those rectangles is supposed to be the trunk rectangle. That would then be the rightmost triangle. That would also match the scale in which the 3rd picture is drawn. And it means the tree grows bigger than an A4.
If so, then your justifications are perfect!

It just means that the 2nd picture is misleading. (Crying)

 

[mathmari]

I believe your justifications are just fine, and I wouldn't know what to improve. (Happy)
I was looking at picture 2 and tried to find the trunk in there.
The best I could find is the rectangle at the bottom with 1/9th of the width and 1/3rd of the height... (Thinking)

Hmm... rereading the OP, it seems intended that after the initial division into 3 rectangles, one of those rectangles is supposed to be the trunk rectangle. That would then be the rightmost triangle. That would also match the scale in which the 3rd picture is drawn. And it means the tree grows bigger than an A4.
If so, then your justifications are perfect!

Ah ok! Great! (Happy)

Then we have the following:

The area of a DIN A4 sheet is equal to $S_0=297\, mm \times 210\, mm=62370 \,mm^2$.

The area of the tree is equal to \begin{equation*}\sum_{i=0}^{\infty}\left (\frac{2}{3}\right )^i\cdot S_1=3\cdot S_1=3\cdot \frac{1}{3}\cdot S_0=S_0=62370\, mm^2\end{equation*}

So the tree has the same area as the sheet, hasn't it? (Wondering)

 

[I like Serena]

Yep.
So it looks like:
View attachment 8110

 

[Olinguito]

Hi mathmari.

So the tree has the same area as the sheet, hasn't it? (Wondering)

I wouldn’t be surprised, since it appears you’re making the tree from just the one sheet, taking nothing out and brining nothing in. (Thinking)

The steps in the construction seem to be as follows:

Step 0: $S_0$

Step 1: $\frac13S_0+\frac23S_0$

Step 2: $\frac13S_0+\frac29S_0+\frac49S_0$

Step 3: $\frac13S_0+\frac29S_0+\frac4{27}S_0+\frac8{27}S_0$​

where the last term in each step is the area to be divided into three in the following step. The total area is thus:
$$\frac13S_0+\frac29S_0+\frac4{27}S_0+\frac8{81}+\cdots$$
$=\ \dfrac13S_0\left[1+\dfrac23+\left(\dfrac23\right)^2+\left(\dfrac23\right)^3+\cdots\right]$

$=\ \dfrac13S_0\cdot\dfrac1{1-\frac23}$

$=\ S_0$.

 

[castor28]

Yes! Looking at that picture, do we have the following?

Let $S_n$ be the area of the rectangular at the $n$-th step.

From each rectangullar of area $S_n$ we get two new rectangulars with total area $\frac{2}{3}\cdot S_n$, i.e. each has area $\frac{1}{3}\cdot S_n$.

This holds because each rectangular gets into three pieces, and two of the three pieces are the branches of the rectanglar.

Let $S_0$ be the area of the DIN A4 sheet. Then $S_1=\frac{1}{3}\cdot S_0$, is the area of the one of the three pieces, which is the root of the tree.

The area of the tree is then equal to
$$S_1+\frac{2}{3}\cdot S_1+\left (\frac{2}{3}\right )^2\cdot S_1+\left (\frac{2}{3}\right )^3\cdot S_1+\ldots=\sum_{i=0}^{\infty}\left (\frac{2}{3}\right )^i\cdot S_1$$Is this correct? Or haven't understood correctly the idea? (Wondering)

Hi mathmari,

Yes, that is correct, and it also gives the answer $3S_1$ for the total area.

This is even simpler than what I had in mind: after all, the fact that the shapes are similar does not matter, the only thing that matters is the ratio of the areas.

 

[mathmari]

Great! Thank you all! (Smile)