Calculate Capacitance with Dielectrics

[screen1998]

Hi, I need help with this.
A non-conducting slab of thickness t, area A and dielectric constant κe is inserted into the space between the plates of a parallel-plate capacitor with spacing d, charge Q and area A, as shown in Figure 7.7.5(a). The slab is not necessarily halfway between the capacitor plates. What is the capacitance of the system?

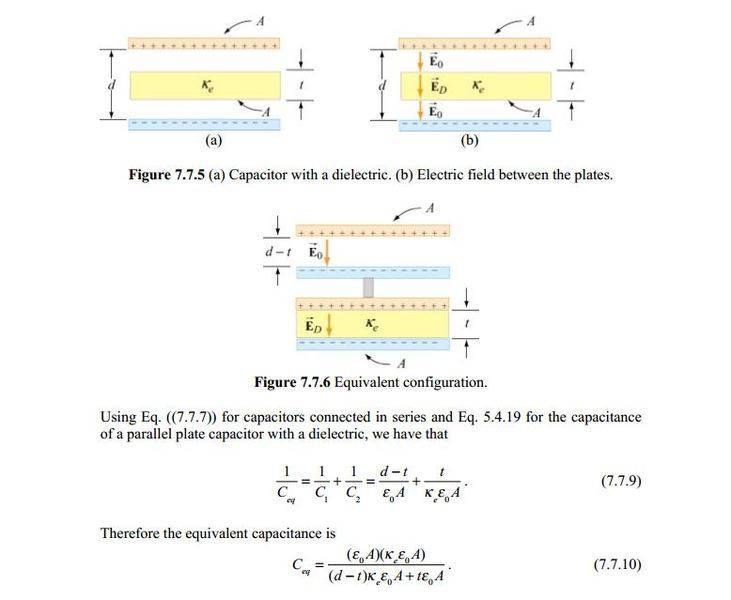
What I don't understand here is the transform from Figurre 7.7.5 to Figure 7.7.6.
How we know that Figure 7.7.6 is the equivalent configuration of Figure 7.7.5?
And why the two dielectrics don't create electric plates because they have different dielectric constants? I know dielectric polarisation but in this case there are two dielectrics with different dielectric constants, therefore I wonder if these electric dipoles will cancel out in the region between two plates of the capacitor.

 

[screen1998]

Any help?

 

[ehild]

Put the slab anywhere - the resultant capacitor is series resultant of three capacitors. Does the result depend to where the slab was placed ?

ehild

 

[screen1998]

Put the slab anywhere - the resultant capacitor is series resultant of three capacitors. Does the result depend to where the slab was placed ?

ehild

Hi ehild,
Could you explain why there are two capacitors in series? What are the sencond plate of these capacitors?

 

[ehild]

The potential is the same along a plane parallel with the capacitor plates. You can substitute an equipotential surface by a thin metal foil- nothing changes.
Putting a dielectric slab of thickness t inside the capacitor at distance d1 from the top plate, and imagining thin metal foils on the top and base faces of the dielectric slab,it is equivalent with three capacitors in series: all with area A, thickness and relative dielectric constant d1,1 ; t, ε, (d-d1-t), 1. The metal foils serve as new plates, see figure. Write up the resultant: you will see that d1 cancels. The resultant capacitance is the same for all d1, it can be even zero, which corresponds to the situation that the dielectric slab touches one plate.

A more basic approach is through the definition of capacitance: It is charge over voltage. Inserting the dielectric slab does not change the charge on the capacitor, but changes the electric field inside the dielectric slab. If it was E without the dielectrics, inside the dielectrics it will be E/ε_r. You get the potential difference between the plates by integrating the electric field along the gap between the plates: it is Ed1+t E/ε_r+E(d-t-d1)=E(d-t)+tE/ε_r. The voltage does not depend on the position of the slab, so you can shift it to one plate and then you get two capacitors in series.

ehild