Homework Help Overview
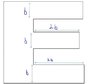
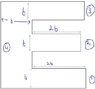
The discussion revolves around calculating the center of mass for a figure of uniform density, specifically by breaking the figure into rectangles and determining their individual centers of mass.
Discussion Character
- Exploratory, Assumption checking, Problem interpretation
Approaches and Questions Raised
- Participants discuss breaking the figure into rectangles and calculating the center of mass for each. Questions arise regarding the mass of each piece and the dimensions of the rectangles. Some participants request clarification on the coordinates and areas of the rectangles.
Discussion Status
Participants are actively engaging in the problem, with some providing their calculations and others seeking further details. Guidance has been offered regarding the relationship between area and mass for uniform density, and there is a suggestion to start the coordinate system from a consistent point for easier calculations.
Contextual Notes
There are indications of missing information regarding the dimensions of the figure and the specific areas of the rectangles, which are essential for calculating the center of mass accurately.